So far we have met just 26 variables, called A to Z. Suppose you wanted to plot a graph showing the mean temperature for every month of the year. You could, at a pinch, use the twelve letters A to L to represent the mean temperatures, and read in the temperatures by saying:
INPUT A,B,C,D,E,F,G,H,I,J,K,L
However there is a much better way. A mathematician might call the list of temperatures by the names:
t1, t2, t3, ..... t12.
where the 'subscript', the number written below the- line, is the number of the month in the year. This representation of the twelve temperatures is much more meaningful than using twelve different letters to stand for them, and there is no doubt about which symbol represents the temperature of, for example, the third month.
A similar series of variables can be created in ATOM BASIC, and these are called 'arrays'. Each array consists of an array 'identifier', or name, corresponding to the name 't' in the above example, and a 'subscript'. On most computers there is no facility for writing subscripts, so some other representation is used. Each member of the array can act as a completely independent variable, capable of holding a value just like the variables A to Z. The members of an array are called the array 'elements'. The total number of possible elements depends on how the array was set up; in the above example there were twelve elements, with subscripts from 1 to 12.
In addition to the standard type of array,
ATOM BASIC provides two other types of array called 'byte
vectors' and 'word vectors'. Byte vectors are useful when only a
small range of numbers are needed, and they use less storage
space than word arrays. Word vectors use the same amount of
storage as arrays, but can be manipulated in a more
flexible manner.
7.1 Arrays - AA to ZZ
The array in ATOM BASIC consists of a pair of identical letters a followed by the subscript in brackets: for example, EE(3). Each element in this type of array can contain numbers as large as the simple variables A to Z, namely, between about -2000 million and 2000 million.
Before an array can be used space must be reserved for it by a DIM, or 'dimension', statement which tells BASIC how large the array - is to be. For example, to reserve space for an array called AA with the five elements AA(0), AA(1), AA(2), AA(3), and AA(4), the statement would be:
DIM AA(4)
The DIM statement allocates space for arrays starting at the first free memory location after the program text. If this were the first a DIM statement encountered in the program the element AA(0) would be at TOP, above the program text:
| TOP: |
|
The question marks represent unspecified values, depending on what the array contained when it was dimensioned. If now another array were dimensioned with the statement:
DIM BB(3)
space for the array BB would be reserved immediately following on from AA.
Array elements can appear in expressions, and be assigned to, just like the simple variables A to Z. For example, to make the value of AA(3) become 776 we would execute:
AA(3)=776
Then we could execute:
AA(1)=AA(3)*2
AA(0)=AA(3)-6
and so on. The resulting array would now be:
| TOP: |
|
There are two places in BASIC programs where array elements may not be used; these are:
1. As the control variable in a FOR...NEXT loop.
2. In an INPUT statement.
In these two cases the simple variables, A to Z, must be used.
The following program illustrates the use of arrays to plot a histogram of the temperature over the twelve months of the year. The temperatures, assumed to be in the range 0 to 100, are first entered in and are stored in the array TT(1..12).
1 REM Histogram 10 DIM TT(12) 20 FOR J=1 TO 12;INPUT K 30 TT(J)=K; NEXT J 40 PRINT $12; CLEAR 0; @=5 50 MOVE 60,12; DRAW 12,12 60 DRAW 12,42 70 FOR N=11 TO 0 STEP -1 80 IF N=7 PRINT "TEMP." 90 IF N%2=0 PRINT N*10 100 PRINT';NEXT N 110 PRINT " JAN MAR MAY JUL SEP NOV"' 120 PRINT " FEB APR JUN AUG OCT DEC"' 130 PRINT " MONTH"' 140 FOR N=1 TO 12; J=11+4*N 150 MOVE J,12; DRAW J,(TT(N)*3/10+12) 160 NEXT N; END
Description of Program: 20-30 Input 12 values 40 Clear screen 50-60 Draw axes 70-100 Label vertical axis 110-130 Label horizontal axis 140-160 Plot histogram bars
Program size: 415 bytes Array storage: 52 bytes
The following program illustrates the use of arrays to sort a series of numbers into ascending order. It uses a fairly efficient sorting procedure known as the 'Shell' sort. The program, as written, reads in 20 numbers, calls a subroutine to sort the numbers into order, and prints the sorted numbers out.
1 REM Sorting
5 DIM AA(20)
10 FOR N=1 TO 20; INPUT J
20 AA(N)=J; NEXT N
30 N=20; GOSUB s
40 FOR N=l TO 20; PRINT AA(N)'
50 NEXT N
60 END
100sM=N
110 DO M=(M+2)/3
120 FOR I=M+1 TO N
130 FOR J=I TO M+1 STEP -M
140 IF AA(J)>=AA(J-M) GOTO b
150 T=AA(J); AA(J)=AA(J-M); AA(J-M)=T
160 NEXT J
170b NEXT I
180 UNTIL M=l; RETURN
Description of Program: 5-20 Read in array of numbers 30 Call Shell sort 40-50 Print out sorted array 100-180 s: Shell sort subroutine 140-150 Swap elements which are out of order.
Variables: AA(1..20) - Array to hold numbers I,J - Loop counters N - Number of elements in array AA M - Subset step size T - Temporary variable
Program size: 332 bytes Array storage: 84 bytes
7.1.3 Arbitrary-Precision Arithmetic
The following program allows powers of two to be calculated to any precision, given enough memory. As it stands the program will calculate all the powers of 2 having less than 32 digits. The digits are stored in an array AA, one digit per array element. Every power of 2 is obtained from the previous one by multiplying every element in the array by 2, and propagating a carry when any element becomes more than one digit.
5 REM Powers of Two 10 DIM AA(31) 20 @=1; P=0 30 AA(0)=1 40 FOR J=1 TO 31 50 AA(J)=0 60 NEXT J 70 DO J=31 80 DO J=J-1; UNTIL AA(J)<>0 85 PRINT'"2^" P "=" 90 FOR K=J TO 0 STEP -1 94 PRINT AA(K) 96 NEXT K 110 C=0 120 FOR J=0 TO 31 130 A=AA(J)*2+C 140 C=A/10 150 AA(J)=A%10 160 NEXT J 170 P=P+1 180 UNTIL AA(31)<>0 190 END
Description of Program: 40-60 Zero array of digits 80 Ignore leading zeros 85-96 Print power 110-160 Multiply current number by 2 180 Stop when array overflows.
Variables: AA - Array of digits; one digit per element C - Decimal carry from one digit to next J - Digit counter K - Digit counter P - Power being evaluated
Program size: 356 bytes Array usage: 124 bytes Total memory: 480 bytes.
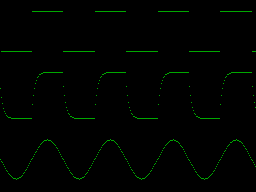
The following program uses a 256-element array to store a waveform which can be low-pass filtered, converted to a square wave, or printed out.
1 REM Digital Waveform Processing
5 DIM AA(255)
10 H=2000
15 CLEAR4
23 GOS.s; GOS.q
25 Z=160; GOS.p
28 GOS.l
30 Z=96; GOS.p
32 GOS.s
34 Z=32; GOS.p
90 END
1000pREM Plot Waveform
1005 MOVE 0,96
1010 FOR N=0 TO 255
1020 PLOT13,N,(Z+AA(N)/H)
1030 NEXT N
1040 RETURN
2000sREM Make Sine Wave
2010 S=0;C=40000
2020 FOR N=0 TO 255
2030 AA(N)=-S
2040 C=C-S/10
2050 S=S+C/10
2060 NEXT N
2070 RETURN
3000qREM Make Square Wave
3010 FOR N=0 TO 255
3020 IF AA(N)>=0 AA(N)=40000
3030 IF AA(N)<0 AA(N)=-40000
3035 NEXT N
3040 RETURN
4000lREM Low Pass Filter
4010 B=0
4020 FOR N=0 TO 255
4030 B=AA(N)*360/1000+B*697/1000
4040 AA(N)=B; NEXT N
4050 RETURN
Description of Program: 23 Calculate a square wave 25 Plot it at top of screen 28 Low-pass filter the square wave 30 Plot it in centre of screen 32 Calculate a sine wave 34 Plot it at bottom of screen 1000-1040 p: Plots waveform 2000-2070 s: Calculates a sine wave. 3000-3040 q: Squares-up the waveform 4000-4050 l: Low-pass filters the waveform
Variables: AA(0...255) - Array of points, values between -40000 and 40000. B - Previous value for low-pass filter C - Cosine of waveform H - Scalinq factor for plotting waveforms N - Counter S - Sine of waveform Z - Vertical coordinate for centre of waveform.
Program size: 564 bytes. Array storage: 1024 bytes Total memory: 1588 bytes
Sample plot:
Many BASIC interpreters perform extensive checking whenever an array element is used in a program. For example, if an array were dimensioned:
DIM RR(10)
then every time the array were used the subscript would be checked to make sure that it was both 0 or greater, and 10 or less. Obviously these two checks slow down the execution of a program, and so in ATOM BASIC only the first check is performed, so that only positive subscripts are allowed. It is left to the programmer to ensure that subscripts do not go out of range. Assigning to an array whose subscript is out of range will change the values of other arrays, or strings, dimensioned after that array.
If required, the programmer can easily add array subscript checking; for example, if the array assignment were:
RR(A)=35
the statement:
IF A>10 THEN ERROR
could be added before the assignment to cause an error if the array subscript, A, went out of range.
7.1.6 Multi-Dimensional Arrays
The standard types of array in ATOM BASIC are one-dimensional. In other words, they have just one subscript, and so can be visualised as lying in a straight line; hence the name 'array'.
Sometimes it is convenient to make each element of an array
represent a cell in a square 'matrix'; each element would then
have two subscripts corresponding to the column and row of that
square.
Such two-dimensional arrays are called 'matrices'. Consider the
following representation of a 3 by 6 matrix:
| 0 | 1 | 2 | 3 | 4 | 5 | |
| 0 | ||||||
| 1 | ||||||
| 2 | x |
The whole matrix has 3 x 6 = 18 elements, and the element shown with an X would have the subscripts (2,4).
ATOM BASIC does not have a direct representation for two-dimensional (or higher dimension) arrays, but they are easily represented using the single-dimension arrays AA to ZZ as described in the following sections.
7.1.7 Calculation of Subscripts
To represent a two-dimensional matrix using a one-dimensional array imagine the matrix divided into rows as shown:
|
|
|
The first element of row 1, with subscripts (1,0), follows immediately after the last element of row 0, with coordinates (0,5). Consider the general case where the matrix has M rows numbered 0 to N-l, and N columns numbered 0 to N-1. The matrix can be dimensioned, using a one-dimensional array, with the DIM statement:
DIM XX(M*N-1)
Any array element, with subscripts A and B, can be referenced as:
XX(A*N+B)
In the earlier example the array had dimensions 3 x 6 and so would be dimensioned:
DIM XX(17)
The array element with subscripts (2,4) would be given by: xx(16)
7.1.8 Solving Simultaneous Equations
The following program will solve a number of linear simultaneous equations, using a matrix to hold the coefficients of the equations, and a matrix inversion technique to find the solution. The program prints the solutions as integers, where possible, or as exact fractions.
This method has the advantage over the standard pivotal condensation technique that for integer coefficients the answers are exact integers or fractions.
The example run shown solves the pair of equations:
a + 2b + 1 = 0 4a + 5b + 2 = 0
10 REM Simultaneous Equations
50 INPUT"NUMBER OF EQUATIONS="N
60 I=N*N;J=N*(N+1)
65 DIM AA(I),CC(J),II(N)
70 @=0;FOR I=1TON;FOR J=1TO N+1
80 PRINT"C("I","J")=";INPUT C
90 CC((I-1)*(N+1)+J)=C;NEXT J;NEXT I
100 L=N+1;GOSUB c;E=D;M=l-2*(N%2)
110 PRINT'"SOLUTION:"'
112 IF E<0 E=-E;M=-M
115 IF E=0;PRINT"DEGENERATE!"';END
120 FOR L=1TON;GOSUB c
125 PRINT"X("L")= "
130 A=M*D;B=E;DO A=A%B
140 IF ABS(B)>ABS(A) THEN T=B;B=A;A=T
150 UNTIL B=0;A=ABS(A)
151 P.(M*D)/A;IF E/A<>1 PRINT"/"E/A
155 M=-M;PRINT';NEXT L;END
160cFOR I=1T0N;FOR J=1TON;K=I*N-N+J
170 IF J<L AA(K)=CC(K+I-1)
180 IF J>=L AA(K)=CC(K+I)
190 NEXT J;NEXT I
200dD=0;F=l;S=l
210 FOR J=1TON;II(J)=J;F=F*J;NEXT J
215 GOSUB f
220 FOR H=2TOF;GOSUB e;NEXT H;RETURN
230eI=N-1;J=N
240gIF II(I)>=II(I+1) I=I-1;GOTO g
250hIF II(I)>=II(J) J=J-1;GOTO h
260 GOSUB i;I=I+1;J=N;IF I=J GOTO f
270 DO GOSUB i;I=I+1;J=J-1;UNTIL I>=J
280fP=I;FOR K=1TON;P=P*AA(N*K-N+II(K))
290 NEXT K;D=D+S*P;RETURN
300iK=II(I);II(I)=II(J);II(J)=K
310 S=-S;RETURN
Description of Program:
50-60 Allocate space for matrix
70-90 Read in matrix of coefficients
120-155 Print solutions
130-150 Find GCD of solution, so it is printed in lowest terms
160-190 c: Permute terms to obtain next addition to determinant; i.e.
for 5 equations, starting with (1,2,3,4,5) run through all
permutations to (5,4,3,2,1).
280-290 f: Add in next product to determinant.
300-310 i: Swap terms in permutation.
Variables: AA(1...N*N) - Matrix CC(1...N*N+N) - Matrix of coefficients S - Signature of permutation.
Program Size: 932 bytes. Variable Space: (2*(N*N+N)+3)*4 bytes
Sample run:
>RUN NUMBER OF EQUATIONS=?2 C(1,1)=?1 C(1,2)=?2 C(1,3)=?1 C(2,1)=?4 C(2,2)=?5 C(2,3)=?2
SOLUTION: X(1)= 1/3 X(2)= -2/3
7.2 Byte Vectors Using, '?'
It is sometimes wasteful of memory to allocate space for numbers over the range provided by word arrays so a second type of array representation is provided which only allocates one byte, rather than four bytes, for each array element. These are referred to as 'byte vectors', and they are in effect one-dimensional arrays. Byte vectors differ from word arrays in that they use one of the simple variables A to Z to hold the 'base' address of the array; i.e. the address in memory where the zeroth element of the array will reside. The array subscripts are simply 'offsets' from this base address; i.e. the subscript is added to the base address to give the address of the array element. The vector elements are written as:
A?0, A?1, A?2, ... etc
where A is the simple variable used to hold the base address of the vector, and the number following the question mark is the subscript.
Note that the zeroth element of a byte vector, A?0, is equivalent to ?A, the contents of the location with address A. Similarly A?1 is equivalent to ?(A+1), and so on.
Byte vectors can be dimensioned by the DIM statement; for example, to dimension a byte vector with elements from A?0 to A?11 the statement would be:
DIM A(11)
Because the DIM statement dimensions arrays and vectors from the end of the program onwards, the above DIM statement is equivalent to:
T=TOP; A=T; T=T+12
where T is a variable used to keep track location. Note that space for vectors can be reserved anywhere in memory, as distinct from arrays which can only be assigned from TOP onwards using the DIM statement. For example, to assign space for a vector S corresponding to the screen memory, simply execute:
S=#8000
Elements of this vector would then correspond to locations on the screen; e.g. S?31 is the location corresponding to the top right-hand corner of the screen.
Each element of a byte array can hold a positive number between 0 and 255, or a single character. Strings are simply byte vectors containing characters. Note that the subscript of a byte array can be an arbitrary expression provided that it is enclosed in brackets.
A second representation for word arrays is provided in ATOM BASIC using the word indirection operator '!', and is mentioned here for completeness, although for simple problems involving arrays the word arrays AA to ZZ are probably more convenient. Word vectors are similar to the byte vectors already described, but each element of the vector consists of a word rather than a byte. Each element consists of the base address variable separated from the subscript, or offset, by a 'pling' '!'. Note that the subscript should be incremented by 4 for each element, since each element is offset 4 bytes from the previous one. For example, a word vector W might have the six elements:
W!0, W!4, W!8, W!12, W!l6, W!20.
Space can be dimensioned for word vectors by using the DIM statement, and allowing 4 bytes per element; for example, to provide storage for the above 6 elements, execute:
DIM W(23)
Note that the zeroth element of the vector, W!0, is equivalent to !W.
7.3.1 Prime Numbers
The following program finds all the prime numbers up to 99999. It uses a word vector to store primes already found, and only tests new candidates for divisibility by these numbers:
1 REM Prime Numbers 10 @=8;S=4;Z=0;J=TOP;G=J;!G=3;PW+S 20 FORT=3TO99999STEP2 30cIFT%!G=Z G=J;N. 40 IFT>!G*!G G=G+S;G.c 50 P.T;!P=T;G=J;P=P+S;N. 60 END
Description of Program: 10 Set up vector 20 Test all odd numbers 30 If divisible, try another. 40 Have we tried enough divisors? 50 Must be prime - print it.
Variables: !G - Divisor being tested J - Equal to TOP !P - Vector of divisors S - Bytes per word T - Candidate for prime Z - Constant zero.
Program size: 155 bytes Vector: as required.
A major advantage of word vectors over the word arrays is that their base addresses are available as values, and so can be passed to subroutines. As an example, consider this program:
10 A=TOP; B=A+40 . . 90 P=A; GOSUB p; REM Output A 94 P=B; GOSUB p; REM Output B 98 END
100pREM Print 10 Elements of array P 105 @=8; PRINT ' 110 FOR J=0 TO 39 STEP 4 120 PRINT P!J 130 NEXT J 140 PRINT ' 150 RETURN
In this example subroutine p can be used to print any array by passing its base address over in the variable P; this is known as a 'call by reference' because the subroutine is given a reference to the array, rather than the actual values in the array.
The following program illustrates the use of word vectors to calculate the value of any number raised to any other number exactly, limited only by the amount of memory available. The program stores four decimal digits per word, so that the product of two words will not cause overflow, and the result is calculated as a word vector.
1 REM Arbitrary Precision Powers
5 T=#3BFF
10 H=(T-TOP)/3; DIM P(H),S(H),D(H)
15 H=10000
20 @=0;PRINT'" POWER PROGRAM"
30 PRINT'" COMPUTES Y X, WHERE x>0 AND Y>0"
40 INPUT'" VALUE OF Y"Y," VALUE OF X"X
50 IFX<1ORY<1PRINT" VALUE OUT OF RANGE";RUN
60 N=Y;N=X;GOSUBp
70 PRINT Y" "X"="P!!P;IF!P<8 RUN
90 F.L=!P-4T04STEP-4
95 IFL!P<1000P.0
100 IFL!P<100P.0
110 IFL!P<10P.0
120 P.L!P;N.;RUN
140*
200pJ=M;IFN%2=0J=1
210 R=P;GOS.e;J=M;R=S;GOS.e;IFN=1R.
250 B=S;DOA=B;GOS.m;B=E
255 N=N/2;A=P;IFN%2GOS.m;P=E
260 U.N<2;R.
280*
300m!D=!A+!B+4;F.J=4TO!D+4S.4
310 D!J=0;N.;W=D-4
320 F.J=4TO!B S.4;C=0;G=B!J
325 V=W+J;F.L=4TO!A S.4
330 Q=A!L*G+C+V!L;V!L=Q%H
340 C=Q/H;N.;V!L=C;N.
370 DO!D=!D-4;U.D!!D<>0;E=D;D=A;R.
380*
400e!R=0;DO!R=!R+4;R!!R=J%H
410 J=J/H;U.J<1;R.
Description of Program:
5 Set T to top of lower text space.
10 Divide available memory between P, S, and D
20-40 Read in values of Y and X
50 Disallow negative values
60 Calculate power
70 Print result if fits in one word
90 Print rest of result, filling in leadinq zeros.
140 Blank line to make listing clearer.
200-260 p: Calculates power. Looks at binary representation of X and
for each bit squares B, and if bit is a 1 multiplies P by
current B.
300-370 m: Multiply together the vectors pointed to by A and B and
put the result into the vector pointed to by D. Pointers to
vectors get changed; E points to result.
400-410 e: Unpack J into vector pointed to by R; store number of
words in !R.
Variables: D!0... - Workspace vector H - Radix for arithmetic P!1... - Vector for unpacked result !P - Number of elements used in P S!0... - Workspace vector T - Top of available memory
Program size: 733 bytes. Additional storage: as available. Sample run: >RUN
POWER PROGRAM
COMPUTES Y^X, WHERE X>0 AND Y>0
VALUE OF Y?16
VALUE OF X?64
16^64=115792089237316195423570985008687907853269984665640564039457584007913129639936
A second way of representing two-dimensional arrays is possible using the ATOM's indirection operators '?' and '!'; this avoids the need for a multiplication to calculate the subscript, but does require slightly more storage. The idea is to think of a two-dimensional matrix as a vector of vectors; first a vector is created containing the addresses of the rows of the matrix. For example, for a matrix called X with columns 0 to M, and rows 0 to N, the following statements will set up the vector of row addresses:
DIM X(2*N-1)
FOR J=0 TO N*2 STEP 2; DIM Q(M); X!J=Q; NEXT J
A word array is used to hold the base addresses. Q is a variable used to hold the base address temporarily. Now that the vector of row base addresses has been set up, the element with subscripts A,B is:
X!(A*2)?B