1 Start Here
If you bought the ATOM ready built, together with a power supply and a
cable to connect it to a TV set, then carry on reading. Otherwise you
should refer to the Technical Manual for details of how to assemble an
ATOM kit, and for details of the required accessories.
The ATOM connects to the aerial socket of an ordinary
black-and-white or colour TV set. The ATOM will not affect the normal
operation of the TV in any way. Connect the UHF output from the ATOM
to the aerial socket of the TV set; see Fig. 1. Connect the ATOM's
power supply to a mains socket, and plug the power connector into the
back of the ATOM; again, see Fig. 1. Press the key marked BREAK on the
top right of the ATOM's keyboard. Switch on the TV set, and turn the
set's volume control down. The ATOM makes use af a TV channel that is
not occupied by any TV stations, and it is necessary to tune to this
channel in order to get the correct display from the ATOM. If the TV
set you are usinq has push buttons to select stations, choose an
unused button and tune the TV by rotating the button. If the TV has a
single numbered tuning dial, turn the dial to somewhere near channel
36. Tune in the TV set until the screen is black, with the following
display in the top left-hand corner of the screen:
ACORN ATOM
<_
Adjust the contrast and brightness controls so that the letters are
clearly legible, and tune the TV set carefully until the letters are
sharp and clear.
The '<' sign is called the ATOM's 'prompt'. It indicates that the
computer is waiting for something to be typed in; a command, perhaps,
or a program. The white rectangle, '_', is called the 'cursor'; it
indicates where on the screen the next character you type in will
appear.
l.l What the ATOM Can Do
The ATOM understands the following special words and symbols:
Commands
LIST, LOAD, NEW.
Functions
ABS, BGET, CH, COUNT, EXT, FIN, FOUT, GET, LEN, PTR, RND, TOP.
Connectives
AND, OR, STEP, THEN, TO.
_3_
Statements
BPUT, CLEAR, DIM, DO, DRAW, END, FOR, GOSUB, GOTO, IF, INPUT, LET,
LINK, MOVE, NEXT, OLD, PLOT, PRINT, PUT, REM, RETURN, RUN, SAVE, SGET,
SHUT, SPUT, UNTIL, WAIT.
Operators
!, #, $, &, *, +, -, /, :, < =, >, ?, \, <>, < >=.
These words and symbols will be explained over the course of the next
12 chapters; for the moment just observe that many of these words have
an obvious meaning; for example, try typing:
PRINT "HELLO"
after the '>' prompt sign. Note that the quotation marks are obtained
by holding down the SHIFT key and typing the '2' key. Now type RETURN
to indicate that the line is finished, and the ATOM will do just that:
HELLO>_
To perform calculations you just need to type PRINT followed by the
expression you want to evaluate. For example, try:
PRINT 7+6*2
When you type RETURN the answer will be printed out. You can try
typing anything you like, but any words not on the above lists will
probably cause an error. For example, try typinq:
HELLO
after the ATOM's ','’ prompt. The ATOM will reply with a 'bleep' and
will print:
ERROR 94
which means that HELLO is not one of the statements or commands that
the ATOM understands.
1.2 A Demonstration
Now that you are in control of your ATOM you may like a quick
demonstration of some more complicated things that it can do. No
attempt is made here to explain how these examples work; for that you
will have to read the rest of the first section of this manual.
You can make ATOM do a lot of typing with very little effort; try
entering:
DO PRINT "ATOM-"; UNTIL 0
Note the difference between the '0' of DO, which is the letter '0',
and the '0' at the end of the statement, which is the digit '0' on the
top row of the keyboard. You will have to type the ESC (escape) key,
which is at the top left of the keyboard, to stop this program.
Now try typing in the following line:
DO PRINT $RND&3+8,$8,$128; UNTIL 0
You will need to use the SHIFT key to get some of the special symbols.
This program is longer than one line of the screen, but just keep
typing and it will appear on a second line. Then press RETURN to run
the program. Again, you will have to type ESC to stop this program.
To demonstrate the graphics commands type:
CLEARO; MOVE 10,0; DRAW 60,50
and the ATOM will draw a line on the screen. If you feel like trying a
more complicated graphics program, type in the following:
_4_
CLEAR0;MOVE32,24;Y=l;DOPLOT1,0,Y;PLOT1,Y,O;Y=-Y-2*Y/A.Y;U.O
Press ESC to get back the ATOM's prompt.
To demonstrate the ATOM's assembler enter the following line after
the prompt:
P=320;[INX; LDA 0,X; STA 4B002; JMP 320;]
An assembler listing will be printed out, and the machine code will be
put into memory at 320. To execute the program, type:
LINK 320
and the ATOM will make a buzzing noise. It is playing the random
contents of its memory through its internal loudspeaker. To stop the
program you will have to type BREAK, because it is a machine-code
program.
You may question the usefulness of these examples, but they do
illustrate the wide range of different tasks the ATOM is capable of.
These 'programs' all fitted onto two lines of the display; to see what
you will be able to do with a longer program take a look at the many
examples later on in this manual.
1.3 The Keyboard
The ATOM keyboard is designed to the standard layout generally
accepted in the computer industry; see Fig. 2. In most respects it is
just like the keyboard of an ordinary typewriter, but there are some
important differences. For a start there are several keys not found on
typewriters, such as DELETE, REPT, CTRL, and BREAK. The purpose of
each of these keys will be explained in the following sections.
Another difference is that the letters A-Z will appear in
capitals, rather than lower-case, when they are typed by themselves.
Try typing in the letters 'ABC' and observe that they appear, as you
type them, on the screen:
>ABC_
From now on, in the examples, the cursor will not be drawn in for
simplicity.
1.3.1 SHIFT
Some keys carry two legends. For example, each digit key (except 0)
also has a special symbol or punctuation mark above it. The lower
symbol on each of these keys is obtained by simply typing that key;
the upper symbol is obtained by holding one of the SHIFT keys down,
and typing that key. This aspect of the keyboard is just like a
typewriter.
If the SHIFT key is held down in conjunction with one of the keys
bearing a single legend, such as A-Z and 0, [, etc, then the character
will appear inverted; i.e. as a black character on a white square.
Inverted A-Z correspond to lower case letters, and will be represented
by lower case letters a-z in this manual. Inverted 0, [, \ etc. will
be represented by 0, g, g etc.
1.3.2 LOCK
The LOCK key, when pressed on its own, changes the way the SHIFT key
operates with the letters A-Z. Initially the keyboard will give
inverted A-Z in conjunction with the SHIFT key, and plain A-Z
otherwise. If the LOCK key is now pressed once the keyboard will
normally give inverted A-Z, and will give plain A-Z only when the
SHIFT key is held down. Pressing LOCK again will revert to the
previous state.
_5_
1.3.3 DELETE
The advantage of a TV screen over a piece of paper is that mistakes
can be corrected without trace of the error. The DELETE key will erase
the last character on the line, and the cursor will back up one space.
Mistakes can thus be deleted and retyped with little effort.
1.3.4 RETURN
The RETURN key is a signal to the computer that you have finished
typing in a line of characters. The cursor will move to the start of
the next line, and the computer may respond to what you have typed by
typing out a reply.
1.3.5 Repeat - REPT
If the 'repeat' key, marked REPT, is held down with another key, that
key is typed repeatedly. REPT is useful in conjunction with DELETE to
erase several characters very rapidly. Note that pressing REPT on its
own will have no effect.
1.3.6 Control - CTRL
There are several special functions available from the keyboard which
are obtained by typing certain keys with the 'control' key - marked
CTRL - held down. Only the following two control functions will be
mentioned here:
CTRL-G gives a bleep in the ATOM's loudspeaker.
CTRL-L clears the screen.
1.3.7 BREAK
The BREAK key will reset the computer, and return it to the state it
was in just after switching on. It should not normally be necessary to
type BREAK, but some assembler programs can cause loops which cannot
be stopped in any other way. Note that the contents of memory are
preserved when BREAK is typed, and any stored program can be
recovered.
1.4 Scrolling
When the cursor reaches the bottom of the screen further lines typed
in will cause the screen to 'scroll'; every line is shifted up so that
you always see the last 16 lines of what has been typed, and the top
line of text on the screen will be lost.
1.5 Storing Text
Any line typed after the ATOM's '>' prompt which starts with a number
is not executed, but stored as text in the ATOM's memory. Any type of
input can be stored in this way; it could be the text of a document, a
program in BASIC, an assembler program, or data for a program. This
section shows how to enter a piece of text, which can then be stored
on cassette, edited, or output to a printer. The same method would be
used for entering a program.
The line must start with a line number, which can be any number
within the range 1 to 32767, and there is no need to use consecutive
line numbers for consecutive lines; indeed, it is wise to choose line
numbers spaced by about 10 as you will soon realise. After the line
number you should type the line of text. For example, enter the
following:
_6_
10 IN XANADU DID KUBLA KHAN
20 A STATELY PLEASURE-DOME DECREE:
30 WHERE ALPH, THE SACRED RIVER, RAN
40 DOWN TO A SUNLESS SEA.
Remember to type RETURN at the end of each line. Each line number can
be followed by up to 64 characters; if you try to type more than 64
characters the ATOM will refuse to proceed until you have deleted
some characters.
The reason for spacing line numbers somewhat apart is that it is
then a simple matter to insert new lines between existing lines. For
example, to insert a line before line 40, type:
36 THROUGH CAVERNS MEASURELESS TO MAN
The computer will sort the lines into the right order, according to
their line numbers, irrespective of the order in which you entered them.
1.6 Commands
Commands typed in after the '>' prompt, without a preceding line
number, and followed by RETURN, are executed immediately by ATOM
rather than being stored in its memory. For example, now type the
command:
LIST
This will cause the stored text to be typed out:
10 IN XANADU DID KUBLA KHAN
20 A STATELY PLEASURE-DOME DECREE:
30 WHERE ALPH, THE SACRED RIVER, RAN
36 THROUGH CAVERNS MEASURELESS TO MAN
40 DOWN TO A SUNLESS SEA.
There are several options with the LIST command. For example:
LIST 10 will list line 10 only.
LIST 20,40 will list lines 20 to 40 inclusive.
LIST 20, will list line 20 onwards.
LIST ,30 will list up to line 30.
A listing can be stopped by typing ESC (escape).
1.7 Editing
One powerful feature of the ATOM's text and program storage is that
stored lines can be modified very simply by typing the same line
number followed by the new version. For example, to change line 20 in
the text just type:
20 NEW LINE TWO
and try listing the program again to see the effect.
To delete a line simply type the line number followed by RETURN.
1.8 Other Commands
Some other useful commands are described here:
NEW will clear the stored text so that a new piece of text can be
typed in. It should always be typed before entering a new piece of
text.
OLD can be typed after typing BREAK to retrieve the text previously in
_7_
memory. Note that you should only type OLD if there is already text in
memory.
1.9 Errors
By now you the ATOM will probably have made a 'bleep' followed by the
message:
ERROR X
where X is the error code number. There are two possible reasons for
errors:
1. You typed something, probably a command, that the ATOM was not
expecting or could not interpret.
2. The ATOM was commanded to do something that it could not do.
For example, typing 'ABC' followed by a RETURN will give the error
message:
ERROR 94
which is probably the most common error; it means that 'ABC' was not a
legal command.
Remember that it is impossible to cause physical damage to the
ATOM, whatever you type at the keyboard. The worst you can do is to
lose the stored text, and even that is extremely unlikely. Most errors
are really warnings, and a complete explanation of all the error codes
is given in Chapter 27.
1.10 Saving Text or Programs on Tape
Having entered some stored text into the ATOM's memory, this section
will show how to save this text, and load it back at a later time.
Text and programs can be saved on standard cassette (or
reel-to-reel) tapes using the ATOM's cassette interface. Connect the
cassette output from the ATOM to the input of a cassette recorder, and
the output from tne recorder to the input of the ATOM. The tape load
routine uses software averaging techniques to minimise the likelihood
of errors on loading, and no trouble should be experienced in
transferring tapes from one machine to another.
1.10.1 Setting Up
Before loading and saving files using the cassette interface it is
worth entering the following simple routines to check that the
cassette system is working correctly, and to find out the best setting
of the recorder's volume control.
Enter the following line after the ATON's prompt:
DO BPUT A,88; WAIT; WAIT; WAIT; WAIT; UNTIL 0
Type RETURN and record on the recorder for a few minutes. To stop the
program type ESC (escape). This program has recorded a sequence of Xs,
in coded form, on the tape. If you play it back it should sound like a
series of short buzzes.
Now enter the following line, which is a program to read
characters from the tape and print them on the screen:
DO PRINT Sbget A; UNTIL 0
The dollar symbol is obtained by holding the SHIFT key down and typing
'4'. Press RETURN, rewind the tape, and play back the 'X's that you
recorded. If all is well a stream of 'X's should be printed out, and
adjust the volume setting on the recorder so that no other characters
appear, indicating errors. When you are satisfied that all is well,
_8_
proceed to the next section.
1.10.2 Text Files
The information is stored as a stream of audible tones on tape; each
section of information is referred to as a 'file'. Several different
files can be saved on one tape, and they are identified by having
unique 'filenames'. Filenames can be anything containing up to 16
letters, digits, or spaces: suitable names are "DATA FILE", "22/4/80",
etc.
1.10.3 SAVE
First check that the stored text is still there by typing LIST. To
save the stored text to tape, type:
SAVE "EXAMPLE"
where "EXAMPLE" is the filename chosen for illustration. Type RETURN,
and the message:
RECORD TAPE
will be printed on the screen. Put the tape recorder to record, and
allow the tape to run well past the leader. Now type RETURN (or any
other key) and the cursor will move to the start of the next line,
indicating that the text is being recorded. After a short delay the
'>' prompt will reappear, and you can turn the tape-recorder off.
1.10.4 *CAT
The *CAT command will give a complete catalogue of all the files on a
cassette. The '*' asterisk is used to distinguish the cassette
operating-system commands from the BASIC commands. Rewind the tape and
type:
*CAT
The ATOM will reply with:
PLAY TAPE
and you should then play the tape, and press any key to start the
catalogue. As a file is encountered on the tape the filename will be
printed out, together with additional information about the file:
EXAMPLE XXXX XXXX XXXX XX
where the 'X's represent four numbers which you can ignore for the
moment (see Section 19.3 for details).
When you have finished you can get back to the '>' prompt by
typing CTRL (control).
1.10.5 LOAD
Switch off the ATOM, in order to cause the saved text to be lost, and
then switch on again and type:
LOAD "EXAMPLE"
The ATOM will reply with:
PLAY TAPE
and the tape should be rewound and played, and RETURN pressed. The
computer will search through the tape for a file of the specified
filename, EXAMPLE in this case, and then load it into its memory. If
all is well the prompt should reappear, and then typing:
LIST
_9_
will give a listing of the text that was previously saved.
1.10.6 File Blocks
If you save a long file on tape, and play it back, you will discover
that it is broken up into a number of short blocks, with gaps in
between, and that when the file is catalogued its name appears several
times, once for each block. This is done for greater reliability, and
if the tape is damaged in the middle of one block it will still be
possible to load back the other blocks of the file.
One further message that may be given when loading tapes is:
REWIND TAPE
This implies that you have started playing the tape in the middle of
the file you wanted to load. Rewind the tape, press RETURN, and the
message:
PLAY TAPE
will be given again.
1.10.7 Errors when Using Tape
If an error is found when loading back a tape file, the message:
SUM
ERROR 6
is given. This might be caused by bad adjustment of the tape-recorder
playback volume, a damaged or dirty tape, or recording a file over
part of a previous file.
If you choose an invalid name for a file, the message:
NAME
ERROR 118
will be given.
_10_
2 Calculating in BASIC
The ATOM computer understands a language called BASIC which, because
of the ease of writing programs in it, has become the most popular
language for use on small computer systems. BASIC was invented in 1964
at Dartmouth College, New Hampshire, and it stands for Beginner's
All-purpose Symbolic Instruction Code. This chapter introduces some of
the facilities available in the BASIC language.
The BASIC language consists of 'statements', 'operators', and
'functions'. The 'statements' are words like PRINT and INPUT which
tell the computer what you want to do; they are followed by the things
you want the computer to operate on.
The 'operators’ are special symbols such as the mathematical signs
'+’ and '-' meaning 'add' and ’subtract'.
The 'functions' are words like the statements, but they have a
numerical value; for example, RND is a function which has a random
value.
2.1 PRINT
This is by far the most useful BASIC statement; it enables programs to
print out the results of their calculations.
Try typing:
PRINT 7+3
The ATOM will print:
10>
The '>' prompt reappears immediately after the answer, 10, is printed
out. This is the best way to use BASIC as a simple calculator; type
PRINT followed by the expression you want to evaluate.
Try the effect of the following:
PRINT 7-3
PRINT 7*3
PRINT 7/3
You will discover that '*’ means multiply; it is the standard multiply
symbol on all computers. Also '/’ means divide, but you may be
surprised that the answer to 7/3 is given as 2, not 2 and 1/2. ATOM
BASIC only deals in whole numbers, or integers, so the remainder after
the division is lost. The remainder can be obtained by typing:
PRINT 7%3
The '%' operator means ’give remainder of division'.
More complex expressions are evaluated according to the standard
rules of mathematics, so the expression:
PRINT 2+3*4-5
has the result 9. Multiplications and divisions are performed first,
followed by additions and subtractions. Round brackets can be used to
I make sure that operations are performed in the correct order; anything
enclosed in brackets is evaluated first. Thus the above expression
could also be written:
_11_
PRINT (2+(3*4))-5
There is no limit to the complexity of expressions that ATOM BASIC can
evaluate, provided they will fit on two lines of the VDU. You will
notice that ATOM BASIC calculates extremely rapidly. Try typing:
PRINT 9*9*9*9*9*9*9*9*9
ATOM BASIC can calculate with numbers between about 2000 million
and -2000 million, which gives an accuracy of between nine and ten
digits. Furthermore, because whole numbers are used, all calculations
in this range are exact.
2.1.1 Printing Several Things
You can print the results of several calculations in one PRINT
statement by separating them with commas:
PRINT 7, 7*7, 7*7*7, 7*7*7*7
which will print out:
7 49 343 2401
Note that each number is printed out on the right-hand side of a
column eight characters wide. This ensures that when large numbers of
results are printed out they will be in neat columns on the screen.
2.1.2 Printing Strings
PRINT can also be used to print out words, or indeed, any required
group of characters. Arbitrary groups of characters are referred to
simply as 'strings', and to identify the characters as a string they
are enclosed in double quotes. For example:
PRINT "THE RESULT"
will cause:
THE RESULT>
to be printed out. The characters in quotes are copied faithfully,
exactly as they appear in the PRINT statement. Thus you could type:
PRINT "55*66=", 55*66
where the expression inside quotes is a string just like any other.
This would print out:
55*66= 3630>
2.2 Variables - A to Z
You will probably be familiar with the use of letters, such as X and
N, to denote unknown quantities. E.g.: "the nth. degree", "X marks the
spot", etc. In ATOM BASIC any letter of the alphabet, A to Z, may be
used to denote an unknown quantity, and these are called 'variables'.
The equals sign '=' is used to assign a particular value to a
variable. For example, typing:
X=6
will assign the value 6 to X. Now try:
PRINT X
and, as expected, the value of X will be printed out. Note the
difference between this and:
PRINT "X"
_12_
The assignment statement 'X=6' should be read as 'X becomes 6' because
it denotes an operation which changes the value of X, rather than a
statement of fact about X. The following statement:
X=X+1
is perfectly reasonable, and adds 1 to the previous value of X. In
words, the new value of X is to become the old value of X plus one.
Now that we can use variables to stand for numbers, they can also
be used in expressions. For example, to print the first four powers of
12 we can type:
T=12
PRINT T, T*T, T*T*T, T*T*T*T
2.3 Getting the Right Answer
Suppose you wanted to calculate half of 777. You might type:
PRINT 777/2
and you would get the answer 388. Then, to get the remainder, you
would type:
PRINT 777%2
and the answer will be l. So the exact answer is 388 and one half.
Suppose, however, you decided to try:
PRINT 1/2*777
thinking it would give 'a half times 777', you would be surprised to
get the answer 0. The reason lies in tie fact that the calculation is
worked out from left to right in several stages, and at every stage
only the whole-number part of the result is kept. First 1/2 is
calculated, and the result is 0 because the remainder is not saved.
Then this is multiplied by 777 to give 0!
Fortunately there is a simple rule to avoid problems like this:
Do Divisions Last!
The division operation is the only one that can cause a loss of
accuracy; all the other operations are exact. By doing divisions last
the loss of accuracy is minimised.
Applying this rule to the previous example, the division by two
should be done last:
PRINT (1*777)/2
which is obviously the same as what was written earlier.
2.3.1 Fixed-Point Calculations
An alternative way to find half of 777 is to imagine the decimal point
moved one place to the right, and write:
PRINT 7770/2
The result will then be 3885, or, with the decimal point moved back to
the correct place, 388.5. For example, in an accounting program you
would use numbers to represent pence, rather than pounds. You could
then work with sums of up to 20 million pounds. Results could be
printed out as follows:
PRINT R/100, "POllNDS", R%100, "PENCE"
2.4 Print Field Size - '@'
Numbers are normally printed out right-justified in a field of 8
character spaces. If the number needs more than 8 spaces the field
_13_
size will be exceeded, and the number will be printed in full without
any extra spaces. Note that the minus sign is included in the field
size for negative numbers.
It is sometimes convenient to alter the size of the print field.
The variable '@' determines this size, and can be altered for other
field widths. For example:
@=32
will print one number per line, because there are 32 character
positions on each line.
The value of '0’ can be zero, in which case no extra spaces will
be inserted before the numbers.
2.5 Printing a New Line
A single quote in a PRINT statement will cause a return to the start
of the next line. Thus:
PRINT "A" ' "T" ' "0" ' "M"
will print out:
A
T
0
M
>
This is an improvement over most other versions of BASIC, which would
require four separate PRINT statements for this example.
2.6 Multiple-Statement Lines - ';'
ATOM BASIC allows any number of statemerits to be strung together on
each line provided they are separated by semicolons. For example the
following line:
A=1;B=2;C=3;PRINT A,B,C'
will print:
1 2 3
2.7 Hexadecimal Numbers
Numbers can also be represented in a notation called 'hexadecimal'
which is especially useful for representing addresses in the computer.
Hexadecimal notation is explained in section 13.1.1; all that needs to
be mentioned here is that hexadecimal notation is just an alternative
way of writing numbers which makes use of the digits 0 to 9 and the
letters A to F. The '0' symbol, called 'hash', is used to introduce a
hexadecimal number. Thus Oe9 is a perfectly good hexadecimal number
(nothing to do with the variable E).
PRINT #8000
will print:
32768>
The PRINT statement prints the number out in decimal. 08000 is the
address of the display area, and is a more convenient way of
specifying this address than its decimal equivalent.
A number can be printed in hexadecimal by prefixing it with an ’&'
ampersand in the PRINT statement. Thus:
PRINT &32768
_14_
will print:
8000>
2.8 Logical Operations
In addition to the arithmetic operations already described, ATOM BASIC
provides three operations called 'logical operations': '&' (AND), '\'
(OR), and ':' (Exclusive-OR). These are all operations between two
numbers, so there is no danger of confusing this use of '&' with its
use to specify printing in hex as covered in the previous section.
These are especially useful when controlling external devices from a
BASIC program. Note that the '\' symbol is obtained on the keyboard by
typing ’shift \', and it will appear on the display as an inverted
'\' ·
The following table gives the results of these three operations
for the numbers 0 and 1:
Operands
A B |
A & B |
A \ B |
A:B |
| 0 0 |
0 |
0 |
0 |
| 0 1 |
0 |
1 |
1 |
| 1 0 |
0 |
1 |
1 |
| 1 1 |
1 |
1 |
0 |
Try typing the following:
PRINT 0 & 1
PRINT 1 \ 1
PRINT 1 : 1
and verify that the results agree with the table.
2.9 Peeking and Poking
Many BASICs have PEEK and POKE functions which do the following:
PEEK looks at the contents of a place in memory, or memory location
POKE changes the contents of a memory location.
The '?' operator, called 'query', is used for poking and peeking in
ATOM BASIC and it provides a more elegant mechanism than the two
functions provided in other BASICs.
The contents of some memory location whose address is A is given
by typing:
PRINT ?A
For example, to look at the contents of location OCOOO type:
PRINT ?#COOO
and the result will be 60 (this is the first location in the ATOM
ROM).
To change the contents of a location whose address is A to 13 just
type:
?A=13
For example, to change the contents of the memory location
corresponding to the top left-hand corner of the screen type:
_15_
?#8000=127
and a white block will appear in the top left of the screen (see
section 18.5 for an explanation).
As another useful example try:
?#EI=0
which will turn the cursor off. To turn the cursor back on again type:
?#E1=#80
_16_
3 Planning a Program
The first step in writing a program, whether it will eventually be
programmed in BASIC or Assembler, is to express your problem in terms
of simple steps that the computer can understand.
The Atom could be put to an immense number of different uses;
anything from solving mathematical problems, controlling external
equipment, playing games, accounting and book-keeping, waveform
processing, document preparation...etc. The list is endless. Obviously
all these applications cannot be included in a computer's repertoire
of operations. Instead what is provided is a versatile set of more
fundamental operations and functions which, in combination, can be
used to solve such problems.
It is therefore,up to you to become familiar with the fundamental
operations that are provided, and learn how to solve problems by
combining these operations into programs.
Programming is rather like trying to explain to a novice cook, who
understands little more than the meanings of the operations 'stir',
'boil’, etc, how to bake a cake. The recipe corresponds to the
program; it consists of a list of simple operations 'stir', 'bake',
with certain objects such as 'flour', 'eggs':
Recipe 1. Sponge Cake
1. Mix together 4 oz. sugar and 4 oz. butter.
2. Stir in 2 eggs.
3. Stir in 4 oz. flour.
4. Put into tins.
5. Bake for 20 mins. at Mark 4.
6. Remove from oven and eat.
7. END
The recipe is written so that, provided all the ingredients are
already to hand, the cook can follow each command in turn without
having to look ahead and worry about what is to come.
Similarly, a computer only executes one operation at a time, and
cannot look ahead at what is to come.
3.1 Flowcharts
Before writing a program in BASIC or Assembler it is a good idea to
draw a 'flowchart' indicating the operations required, and the order
in which they should be performed. The generally accepted standard is
for operations to be drawn inside rectangular boxes, with lines
linking these boxes to show the flow of control. A simple flowchart
for the program to bake a cake might be drawn as follows:
_17_
3.2 Decisions
Many recipes do not just contain a sequence of steps to be performed,
but contain conditions under which several different courses of action
should be taken. For example, for a perfect cake line 5 would be
better written:
5. Bake until golden brown.
It would then be necessary to open the oven door every five minutes
and make a decision about the colour of the cake. Decisions are
represented in flowcharts by diamond-shaped boxes, with multiple exits
labelled with the possible outcomes of the decision. The new flowchart
would then be:
_18_
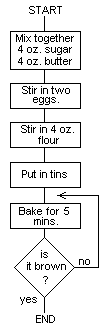
The action 'bake for 5 mins.' is repeatedly performed until the test
'is it brown?' gives the answer 'yes'. Of course the program would go
dramatically wrong if the oven were not switched on; the program would
remain trapped in a loop.
With these two simple concepts, the action and the decision,
almost anything can be flowcharted. Part of the trick in flowcharting
programs is to decide how much detail to put into the flowchart. For
example, in the cake program it would be possible to add the test 'is
butter and sugar mixed?' and if not, loop back to the operation 'mix
butter and sugar'. Usually flowcharts should be kept as short as
possible so that the logic of the program is not obscured by a lot of
unnecessary fine detail.
3.3 Counting
Recipes sometimes require a particular series of operations to be
performed a fixed number of times. The following recipe for puff
pastry illustrates this:
Recipe 2. Puff Pastry
1. Mix 6 oz. flour with 2 oz. butter.
2. Roll out pastry.
3. Spread with 2 oz. butter.
_19_
4. Fold in half.
5. Repeat steps 2 to 4 a further 3 times.
6. END
In this recipe the cook has to perform operations a total of 4 times.
A cook would probably keep a mental note of how many times he has
performed these operations; for the sake of the flowchart it is
convenient to give the number of operations a label, such as T. The
flowchart of the puff pastry recipe would then be:
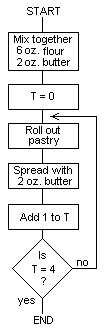
The loop consisting of statements 2 to 4 is performed 4 times; the
test at the end gives the answer 'no' for T=l, 2, and 3, and the
answer 'yes' for T=4.
To perform an operation several times in a BASIC or Assembler
program an identical method can be used; a counter, such as T, is used
to count the number of operations and the counter is tested each time
to determine whether enough operations have been completed.
3.4 Subroutines
A recipe may include a reference to another recipe. For example, a
typical recipe for apple tart might be as follows:
_20_
Recipe 3. Apple Tart
1. Peel and core 6 cooking apples.
2. Make pastry as in recipe 2.
3. Line tart tin with pastry.
4. Put in apple.
5. Bake for 40 mins. mark 4.
6. END
To perform step 2 it is necessary to insert a marker in the book at
the place of the original recipe, find the new recipe and follow it,
and then return to the original recipe and carry on at the next
statement.
In computer programming a reference to a separate routine is
termed a 'subroutine call'. The main recipe, for apple tart, is the
main routine; one of its statements calls the recipe for puff pastry,
the subroutine. Note that the subroutine could be referred to many
times throughout the recipe book; in the recipe for steak and kidney
pie, for example. One reason for giving it separately is to save
space; otherwise it would have to be reproduced for every recipe that
needed it.
Note that, in order not to lose his place, the cook needed a
marker to insert in the recipe book so that he should know where to
return to at the end of the subroutine. In BASIC or assembler programs
the computer keeps a record of where you were when you call a
subroutine, and returns you there automatically at the end of the
subroutine. In other respects, the process of executing a subroutine
on a computer is just like this analogy.
3.5 Planninq a Program
Before writing a program in BASIC or Assembler it is a good idea to
express the problem in one of the forms used in this chapter:
l. As a list of numbered steps describing, in words, exactly what to
do at each step.
2.As a flowchart using the following symbols:
Having done this, the job of writing the program in BASIC or Assembler
will be relatively easy.
_21_
_22_
4 Writing a BASIC Program
Commands and statements typed after the ATOM's prompt are executed
immediately, as we have seen in Chapter 3. However if you start the
line with a number, the line is not executed but stored as text in the
ATOM's memory.
4.1 RUN
First type 'NEW' to clear the text area. Then try typing in the
following:
10 PRINT "A PROGRAM!"
20 END
When these lines have been typed in you can list the text by typing
LIST. Now type:
RUN
The stored text will be executed, one statement at a time, starting
with the lowest-numbered statement, and the message 'A PROGRAM!' will
be printed out. The text you entered formed a 'program', and the
program was executed, statement by statement, when you typed RUN. The
END statement is used to stop execution of the program; if it is
ommitted an error message will be given.
4.2 INPUT
Type NEW again, and then enter the following program:
10 INPUT N
20 N=N+1
30 PRINT N
The INPUT statement enables you to supply numbers to a running
program. When it is executed it will print a question mark and wait
for a number to be typed in. The variable specified in the INPUT
statement will then be set to the value typed in. To illustrate, type:
RUN
The program will add 1 to the number you type in; try running it again
and try different numbers.
The INPUT statement may contain more than one variable; a question
mark will be printed for each one, and the values typed in will be
assigned to the variables in turn.
The INPUT statement may also contain strings; these will be
printed out before each question mark. The following program
illustrates this; it converts Farenheit to Celsius (Centigrade),
giving the answer to the nearest degree:
10 INPUT "FARENHEIT" F
20 PRINT (10*F-315)/18 "CELSIUS"
30 END
_23_
The value, in Farenheit, is stored in the variable F. The expression
in the PRINT statement converts this to Celsius.
4.3 Comments - REM
The REM statement means 'remark’; everything on the line following the
REM statement will be ignored when the program is being executed, so
it can be used to insert comments into a program. For example:
5 REM PROGRAM FOR TEMPERATURE CONVERSION
4.4 Functions
Functions are operations that return a value. Functions are like
statements in that they have names, consisting of a sequence of
letters, but unlike statements they return a value and so can appear
within expressions.
4.4.1 RND
The RND function returns a random number with a value anywhere between
the most negative and most positive numbers that can be represented in
BASIC. To obtain smaller random numbers the '%' remainder operator can
be used; for example:
PRINT RND%4
will print a number between -3 and +3.
4.4.2 TOP
TOP returns the address of the first free memory location after the
BASIC program.
PRINT &TOP
will print TOP in hexadecimal. This will be 48202 if you have not
entered a program (or have just typed NEW) on the unexpanded ATOM, and
#2902 on an expanded ATOM.
PRINT TOP-#8200
is a useful way of finding out how many bytes are used up by a
program; on an unexpanded ATOM there is a total of 512 bytes for
programs.
4.4.3 ABS
The ABS function can be used to give the absolute or positive value of
a number; the number is written in brackets after the function name.
For example:
PRINT ABS(-57)
will print 57. One use of ABS is in generating positive random
numbers. For example:
PRINT ABS(RND)%6
gives a random number between 0 and 5.
4.5 Escape - ESC
It is possible to create programs which will never stop; see the
following example in section 4.6. The escape key 'ESC' at the top
left of the keyboard will stop any BASIC program and return control to
the '>' prompt.
_24_
4.6 GOTO
In the above programs the statements were simply executed in ascending
order of their line numbers. However it is sometimes necessary to
transfer control forwards or backwards to somewhere other than the
next numbered statement. The GOTO (go to) statement is used for this
purpose; the GOTO statement specifies the statement to be executed
next. For example, type:
1 REM Stars
10 PRINT "*"
20 GOTO 10
A flowchart for this program makes it clear that the program will
never stop printing stars:
To stop the program you will have to type ESC (escape).
4.6.1 Labels - a to z
ATOM BASIC offers another option for the GOTO statement. Instead of
giving the number of the statement to be executed next, a statement
can be designated by a 'label', and the GOTO is followed by the
required label.
A label can be one of the lower-case letters a to z, which are
obtained on the ATOM by typing the letter with the shift key held
down. Labels appear on the VDU as upper-case inverted letters, so they
are very easily identified in programs. For typographical convenience
labels will be represented as lower-case letters in this manual.
To illustrate the use of labels, rewrite the ’STARS' program as
follows, using the label 's':
10s PRINT "*"
20 GOTO s
Note that there must be no spaces between the line number and the
label.
There are two advantages to using labels, rather than line
numbers, in GOTO statements. First, programs are clearer, and do not
depend on how the program lines are numbered. Secondly, the GOTO
statement is faster using a label than using a line number. To
demonstrate this, enter the following program which generates a tone
of 187 Hz in the loudspeaker:
10 P=#B002
20a ?P=?P:4; GOTO a
This program works as follows: P is the location corresponding to the
input/output port, and exclusive-ORing this location with 4 will
change the output line connected to the loudspeaker. The frequency
generated implies that the statements on line 20 are executed in about
2.5 milliseconds (twice per cycle).
_25_
Try removing the label and rewrite the program as follows:
10 P=OB002
20 ?P=?P:4; GOTO 20
The GOTO statement is now slightly slower, and the tone generated will
have the lower frequency of 144 Hz. The highest frequency that can be
generated by a BASIC program is 322 Hz, as follows:
10 REM 322 Hz
20 P=#B002
30 FOR Z=O TO 10000000 STEP 4;?P=Z;N.
To play tunes you will need to use an assembler program; see Section
15.4.
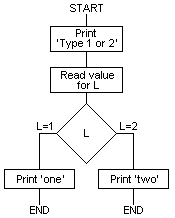
4.6.2 Switches
The GOTO statement may be followed by any expression which evaluates
to a valid line number; for example:
10 REM Two-Way Switch
20 INPUT "TYPE 1 OR 2" L
30 GOTO (40*L)
40 PRINT "ONE"
50 END
80 PRINT "TWO"
90 END
If L is 1 the expression (40*L) will be equal to 40, and the program
will print 'ONE'. If L is 2 the expression will be equal to 80 and the
program will print 'TWO’. The flowchart for this program is as
follows:
4.6.3 Multi-Way Switches
Finally here is an example of a multi-way switch using GOTO. The
program calculates a random number between 0 and 5 and then goes to a
_26_
line number between 30 and 35. Each of these lines consists of a PRINT
statement which prints' the face of a dice. The single quote in the
print statement gives a 'return' to the start of the next line.
10 REM Dice Tossing
20 GOTO (30+ABS(RND)%6)
30 PRINT'" *"''; END
31 PRINT" *"''"*"'; END
32 PRINT" *"'" *”’”*"'; END
33 PRINT"* *”''"* *"’; END
34 PRINT"* *"'" *"'”* *"'; END
35 PRINT"* *"'"* *"'"* *"'; END
Description of Program:
20 Choose random number between 30 and 35
30-35 Print corresponding face of a dice Sample runs:
>RUN
*
*
*
>RUN
* *
*
* *
>RUN
* *
* *
* *
4.7 Graphics
The ATOM has no less than 9 different graphics modes available from
BASIC. This section provides a brief introduction to graphics mode 0,
the lowest resolution mode, which is available on the unexpanded ATOM.
With more memory added to the ATOM the other graphics modes are
available, and these are explained in Chapter 11. A special feature of
mode 0 is that it is possible to mix graphics with any of the ATOM's
characters.
Graphics treats the screen as a piece of graph paper on which it
is possible to draw lines and plot points. Points on the screen are
called 'picture elements' or ’pixels' for short, because they are
actually small squares. Each pixel on the screen is specified by its
coordinates in the two directions, horizontal and vertical, and these
coordinates will be referred to as X and Y respectively. The graphics
screen is labelled as follows in mode 0:
| 0,47 |
|
63,47 |
^
|
Y
| |
 |
|
| 0,0 |
-- X --> |
63,0 |
_27_
4.7.1 CLEAR
To prepare the screen for graphics the statement CLEAR is used. It is
followed by the graphics mode number. On the unexpanded ATGN the only
legal option is:
CLEAR 0
4.7.2 MOVE
Any point on the screen can be specified by moving the 'graphics
cursor' to that point with the MOVE statement. The graphics cursor
does not show on the screen, and it is different from the ordinary
cursor which is visible in character mode. The format of the statement
is:
MOVE X,Y
where X and Y can be numbers, or arbitrary expressions provided they
are enclosed in brackets. For example, to move the graphics cursor to
the origin, X=0 Y=O, type:
MOVE 0,0
The MOVE statement will normally be the first graphics statement of
any program.
4.7.3 DRAW
The DRAW statement will plot a line anywhere on the screen. The line
starts from the position of the graphics cursor, and ends at the point
specified in the statement, and tie graphics cursor will be moved to
that point. For example:
DRAW 63,47
will draw a line to the top right-hand corner of the screen, and leave
the graphics cursor at that point. It is quite legal, and safe, to
draw off the screen; the line will just not appear.
4.7.4 Example
The following simple program will draw a rectangle, rotated by the
amount entered for R. Try typing in numbers between 0 and 47 for R:
10 REM Rotating Rectangle
20 x=63; Y=47
30 INPUT R
40 CLEAR 0
50 MOVE R,O
60 DRAW X,R; DRAW (X-R),Y
70 DRAW 0,(Y-R); DRAW R,O
80 GOTO 30
4.7.5 Plotting Points
One way of plotting a single point at X,Y on the screen is to write:
MOVE X,Y; DRAW X,Y
A more elegant way is given in Section 11.3.
4.8 Conditions - IP...THEN
One of the most useful facilities in BASIC is the ability to execute a
statement only under certain specified conditions. To do this the
IF...THEN statement is used; for example:
_28_
IF A=0 THEN PRINT "ZERO"
will execute the PRINT statement, and print "ZERO", only if the
condition A=0 is true; otherwise everything after THEN will be skipped
and execution will continue with the next line.
4.8.1 Relational Operators
The part of the IF...THEN statement after the IF is the 'condition'
which can be any two expressions separated by a 'relational operator'
which compares the two expressions. Six different relational operators
can be used:
= equal << not equal
< greater than <="less than or equal
< less than"<= greater than or equal
where each operator on the left is the opposite of the operator on the
right.
The expressions on each side of the relational operators can be as
complicated as required, and the order is unimportant. There is no
need to put brackets around the expressions.
For example, the following program prints one of three messages
depending on whether a number typed in is less than 7, equal to 7, or
greater than 7:
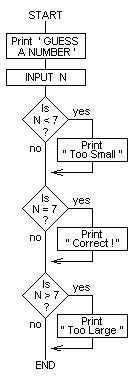
10 REM Guess a number
20 INPUT"GUESS A NUMBER" N
30 IF N<7 then print ntoo small"
40 if n="7 THEN PRINT CORRECT!
50 IF N">7 THEN PRINT "TOO LARGE"
60 END
A flowchart for this program is as follows:
_29_
4.8.2 THEN Statement
The statement after THEN can be any statement, even an assignment
statement as in:
IF A=7 THEN A=6
Note that the meaning of each '=' sign is different. The first 'A=7'
is a condition which can be either true or false; the second 'A=6' is
an assignment statement which instructs the computer to set the
variable A to the value 6. To make this distinction clear the above
statement should be read as: 'If A is equal to 7 then A becomes 6'.
4.8.3 Conjunctions - AND and OR
Conditions can be strung together using the conjunctions AND and OR,
so, for example:
10 INPUT A,B
20 IF A=2 AND B=2 THEN PRINT "BOTHI 30 GOTO 10
_30_
will only print "BOTH" if both A and B are given the value 2.
Alternatively:
10 INPUT A,B
20 IF A=2 OR B=2 THEN PRINT ”EITHER"
30 GOTO 40
will only print "EITHER" if at least one of A and B is equal to 2.
4.9 Logical Variables
An alternative form for the condition in an IF...THEN statement is to
specify a variable whose value denotes either 'true' or 'false'. The
values 'true’ and 'false' are represented by 1 and 0 respectively, so:
A=1; B=0
sets A to 'true' and B 'false'. Logical variables can be used in place
of conditions in the IF statement; for example:
IF A THEN PRINT "TRUE"
will print "TRUE".
A logical variable can also be set to the value of a condition:
A=(L=100)
This statement will set A to 'true' if L is 100, and to 'false’
otherwise. The condition must be placed in brackets as shown.
4.10 Iteration
One way of printing the powers of 2 would be to write:
10 REM Powers of Two
20 P=1; T=2; @=0
30 PRINT "2 ", P, "= ", T '
40 T=T*2; P=P+1
50 GOTO 30
which will print out:
2 ^ 1 = 2
2 ^ 2 = 4
2 ^ 3 = 8
2 ^ 4 = 16
2 ^ 5 = 32
2 ^ 6 = 64
and so on without stopping. This is a bit inelegant; suppose we wished
to print out just the first 12 powers of 2. It is simply a matter of
detecting when the 12th. power has just been printed out, and stopping
then. This can be done with the IF statement as follows:
10 REM First Twelve Powers of Two
20 P=l; T=2; @=0
30 PRINT "2" ^, P, " = ", T '
40 T=T*2; P=P+1
50 IF PC=12 GOTO 30
60 END
The IF statement is followed by a GOTO statement; if P is less than 12
the condition will be true, and the program will go back to line 30.
_31_
After the twelth power of 2 has been printed out P will have the value
13, which is not less than or equal to 12, and so the program will
stop.
With the IF statement we have the ability to make the computer do
vast amounts of work as a result of very little effort on our part.
For example we can print,256 exclamation marks simply by running the
following program:
10 I=0
20 PRINT"!"; I=I+1
30 IF I<256 goto 20
40 end
4.10.1 Cubic Curve
Perhaps a more useful example is the following program, which
calculates the value of:
x^3 - 600x
for 64 values of x and plots a graph of the resulting curve:
1 REM Cubic Curve
10 CLEAR 0
20 MOVE 0,24; DRAW fi3,24
30 MOVE 32,0; DRAW 32,47
40 MOVE -1,-1
50 X=-33
55 Y=(X*X*X-600*X)/400
60 DRAW (32+X),(24+Y)
70 X=X+1
80 IF X<33 then goto 55
90 end
description of program:
10 use graphics mode 0
20-30 draw axes
40 move graphics cursor off screen
50-80 plot curve for values of x from -32 to 32
55 equation to be evaluated divided by 400 to bring the
interesting part of the cubic curve into range
60 draw to next point, with origin at (32,24).
program size: 190 bytes
_32_
5 Loops
The previous section showed how the IF statement could be used to
cause the same statements to be executed several times. Recall the
program:
10 I=0
20 PRINT"!"; I=I+1
30 IF I<256 goto 20
40 end
which prints out 256 exclamation marks (half a screen full). this
iterative loop is such a frequently-used operation in basic that all
basics provide a special pair of statements for this purpose, and atom
basic provides a second type of loop for greater flexibility.
5.1 FOR...NEXT Loops
The FOR statement, together with the NEXT statement, causes a set of
statements to be executed for a range of values of a specified
variable. To illustrate, the above example can be rewritten using a
FOR...NEXT loop as follows:
10 FOR I=1 TO 256
20 PRINT "!"
30 NEXT I
40 END
The FOR statement specifies that the statements up to the matching
NEXT statement should be executed for each value of I from 1 to 256
(inclusive). In this example there is one statement between the FOR
and NEXT statements, namely:
PRINT "!"
This statement has been indented in the program to make the loop
structure clearer; in fact the spaces are ignored by BASIC.
The NEXT statement specifies the variable that was specified in
the corresponding FOR statement. This variable, I in the above
example, is called the 'control variable' of the loop; it can be any
of the variables A to Z.
The value of the control variable can be used inside the loop, if
required. To illustrate, the following program prints out all
multiples of 12 up to 12*12:
10 FOR M=1 TO 12
20 PRINT M*12
30 NEXT M
40 END
The range of values specified in the FOR statement can be anything you
wish, even arbitrary expressions. Remember, though, that the loop is
always executed at least once, so the program:
_33_
10 FOR N=1 TO 0
20 PRINT N
30 NEXT N
40 END
will print '1' before stopping.
5.1.1 STEP Size
It is also possible to specify a STEP size in the FOR statement; the
STEP size will be added to the control variable each time round the
loop, until the control variable exceeds the value specified after TO.
If the STEP size is omitted it is assumed to be 1. This provides us
with an alternative way of printing the multiples of 12:
10 FOR M=12 TO 12*12 STEP 12
20 PRINT M
30 NEXT M
40 END
5.1.2 Graph Plotting Using FOR...NEXT
The FOR...NEXT loop is extremely useful when plotting graphs using the
ATOM's graphics facilities. Try rewriting the Cubic Curve program of
Section 4.10.1 using a FOR...NEXT loop.
The following curve-stitching program is quite fun, especially in
the higher graphics modes. It simulates the curves produced by
stitching with threads stretched between two lines of holes in a
square of cardboard. The curve produced as the envelope of all the
threads is a parabola:
1 REM Curve Stitching in a Square
10 V=46
20 INPUT Q
30 CLEAR 0
40 FOR Z=O TO V STEP Q; Y=V-Z
50 MOVE O,Z; DRAW Y,O
60 MOVE Y,V; DRAW V,Z
70 NEXT Z
80 END
The value of Q typed in should be between 2 and 9 for best results; V
determines the size of the square that is drawn. The program works
best when V is a multiple of Q.
5.2 DO...UNTIL Loops
ATOM BASIC provides an alternative pair of loop-control statements: DO
and UNTIL. The UNTIL statement is followed by a condition, and
everything between the DO statement and the UNTIL statement is
repeatedly executed until the condition becomes true. So, to print 256
exclamation marks in yet another way write:
10 I=0
20 DO
30 I=I+1
40 PRINT "!"
50 UNTIL I=256
50 END
Again, the statements inside the DO...UNTIL loop may be indented to
make the structure clearer.
_34_
The DO...UNTIL loop is most useful in cases where a program is to
carry on until certain conditions are satisfied before it will stop.
To illustrate, the following program prompts for a series of numbers,
and adds them together. When a zero is entered the program terminates
and prints out the sum:
10 S=O
20 DO INPUT J
30 S=S+J
40 UNTIL J=O
50 PRINT "SUM =", S
60 END
Note that a statement may follow the DO statement, as in this example.
5.2.1 Greatest Common Divisor
The following simple program uses a DO...UNTIL loop in the calculation
of the greatest common divisor (GCD) of two numbers; i.e. the largest
number that will divide exactly into both of them. For example, the
GCD of 26 and 65 is 13. If the numbers are coprime the GCD will be l.
1 REM Greatest Common Divisor
80 INPUT A,B
90 DO A=ASB
100 IFABS(B)>ABS(A) THEN T=B; B=A; A=T
120 UNTIL B=O
130 PRINT "GCD =" A '
140 END
Description of Program:
80 Input two numbers
90 Set A to remainder when it is divided by B
100 Make A the larger of the two numbers
120 Stop when B is zero
130 A is the greatest common divisor.
Variables:
A,B - Numbers
T - Temporary variable
Program size: 137 bytes
The method is known as Euclid’s algorithm, and to see it working
insert a line:
95 PRINT A,B'
The ABS functions ensure that the program will work for negative, as
well as positive, numbers.
5.2.2 Successive Approximation
The DO...UNTIL loop construction is especially useful for problems
involving successive approximation, where the value of a function is
calculated by obtaining better and better approximations until some
criterion of accuracy is met.
The following iterative program calculates the square root of any
number up to about 2,000,000,000. Also shown is the output obtained
when calculating the square root of 200,000,000:
10 REM Square Root
20 INPUT S
_35_
100 Q=s/2
110 DO Q=(Q+S/Q)/2
120 UNTIL (Q-1)*(Q-1)<S AND (Q+1)*(Q+1)>S
130 PRINT Q
140 END
Description of Program:
20 Input number
100 Choose starting value
110 Calculate next approximation
120 Carry on until the square lies between the squares of the
numbers either side of the root.
130 Print square root.
Variables:
Q - Square root
S - Number
Program size: 118 bytes Sample run:
>RUN
?200000000
14142>
5.3 Nested Loops
FOR...NEXT and DO...UNTIL loops may be nested; the following example
will print the squares, cubes, and fourth powers of the numbers 1 to
15 in a neat table:
1 REM Powers of Numbers
5 PRINT" X X^2"
8 PRINT" X^3 X^4"
10 FOR N=1 TO 15
20 J=N
30 FOR M=1 TO 4
40 PRINT J; J=J*N
50 NEXT M
60 NEXT N
70 END
The statements numbered 20 to 50 are executed 15 times, for every
value of N from 1 to 15. For each value of N the statements on line 40
are executed four times, for values of M from 1 to 4. Thus 15*4 or 60
numbers are printed out.
5.3.1 Mis-Nested Loops
Note that loops must be nested correctly. The following attempt at
printing out 100 pairs of numbers will not work:
10 FOR A=1 TO 10
20 FOR B=1 TO 10
30 PRINT A,B
40 NEXT A
50 NEXT B
The program will, if RUN, give an error (ERROR 230). The reason for
the error will become clear if you try to indent the statements within
each loop, as in the previous example.
_36_
5.4 WAIT Statement
ATOM BASIC includes an accurate timing facility, derived from the main
CPU clock. To understand the operation of the WAIT statement, imagine
that the ATOM contains a clock which 'ticks' sixty times a second. The
WAIT statement causes execution to stop until the next clock tick.
Thus it automatically synchronises the program to an accurate time.
The WAIT statement makes it a simple matter to write programs to
give any required delay. For example, the following program gives a
delay of 10 seconds:
FOR N=1 TO 10*60; WAIT; NEXT N
You are perhaps wondering why WAIT does not just give a delay of 1/60
second, rather than waiting for the next clock tick. The reason is
that if only a delay function were provided, you would have to know
exactly how long the other statements in the loop took to execute if
you wanted accurate timinq. In fact, with the WAIT function, all you
need to do is to ensure that the statements in the loop take less than
1/60th. of a second, so as not to miss the next tick.
5.4.1 Digital Clock
The following digital clock displays the time as six digits in the top
left-hand corner of the screen.
10 REM Digital Clock
20 INPUT "TIME" H,MgS
30 PRINT $12; ?#El=0
40 T=((H*100)+M)*100+S
50 DO FOR S=l TO 55; WAIT; NEXT S
60 PRINT $30,T; T=T+1
70 IF T%100=60 THEN T=T+40
80 IF T%10000=6000 THEN T=T+4000
90 UNTIL 0
Description of Program:
20 Input the starting time
30 Clear screen; turn off cursor
40 Set up time as 6-digit number
50 Use up rest of a second
60 Print T in top left-hand corner of screen
70-80 Update minutes and hours
Variables:
H - Hours
M - Minutes
S - Seconds
T - Six-digit number representing time
Program size: 216 bytes
To turn the cursor back on after running this program type a
form-feed; i.e. CTRL-L.
5.4.2 Reaction Timer
The following reaction-timer program uses WAIT to calculate your
reaction time, and prints out the time in centiseconds (i.e.
hundredths of a second) to the nearest 2 centiseconds. It blanks the
screen, and then, after a random delay, displays a dot at a random
place on the screen. When you see the dot you should press the SHIFT
key as quickly as possible; the program will then display your
reaction time.
_37_
1 REM Reaction Timer
10 CLEAR 0
20 X=ABS(RND)%64; Y=ABS(RND)%48
30 FOR N=l TO ABS(RND)%600+300
40 WAIT; NEXT N
50 MOVE X,Y; DRAW X,Y
60 T=O
70 DO T=T+1; WAIT
80 UNTIL ?#Bool<>#FF
90 PRINT "REACTION TIME ="
100 PRINT T*10/6, "CSEC."
110 IF T>18 PRINT "WAKE UP!" 120 END
Description of Program:
20 Choose random X,Y coordinates for point on screen.
30-40 Wait for random time between 6 and 9 seconds.
50 Plot point at X,Y
60-70 Count sixtieths of a second
80 #b001 is the address of the input port to which the SHIFT key
is connected; the contents of this location are #ff until
the SHIFT key is pressed.
90-100 Print reaction time converted to centiseconds.
110 If appalling reactions, print message.
Variables:
N - Counter for random delay
T - counter in sixtieths of a second for reaction time
X,Y - random coordinates for point on screen.
Program size: 273 bytes
_38_
6 Subroutines
As soon as a program becomes longer than a few lines it is probably
more convenient to think of it as a sequence of steps, each step being
written as a separate 'routine', an independent piece of program which
can be tested in isolation, and which can be incorporated into other
programs when the same function is needed.
6.1 GOSUB
Sections of program can be isolated from the rest of the program using
a BASIC construction called the 'subroutine'. In the main program a
statement such as:
GOSUB 1000
causes control to be transferred to the statement at line 1000. The
statements from line 1000 comprise the subroutine. The subroutine is
terminated by a statement:
RETURN
which causes a jump back to the main 'calling' program to the
statement immediately following the GOSUB 1000. It is just as if the
statements from 1000 up to the RETURN statement had simply been
inserted in place of the GOSUB 1000 statement in the main program.
As an example, consider the following program:
10 A=10
20 GOSUB 100
30 A=20
40 GOSUB 100
50 END
100 PRINT A '
110 RETURN
Lines 100 and 110 form a subroutine, separate from the rest of the
program, and they are terminated by RETURN. The subroutine is called
twice from the main program, in lines 20 and 40. The program, when
RUN, will print:
6.1.1 Chequebook-Balancing Program
As a more serious example, consider a program for balancing a
chequebook. The program will have three distinct stages; reading in
the credits, reading in the debits, and printing the final amount. We
can immediately write the main program as:
10 REM Chequebook-Balancing Program
20 PRINT "ENTER CREDITS"'
30 GOSUB 1000
_39_
40 PRINT ”ENTER DEBITS"'
50 GOSUB 2000
60 PRINT "TOTAL IS"
70 GOSUB 3000
80 END
Now all we have to do is write the subroutines at lines 1000, 2000,
and 3000!
The subroutines might be written as follows:
1000 REM Sum Credits in C
1010 REM Changes C,J
1020 C=O
1030 DO INPUT J; C=C+J
1040 UNTIL J=O
1050 RETURN
2000 REM Sum Debits in D
2010 REM Changes D,J
2020 D=O
2030 DO INPUT J; D=D+J
2040 UNTIL J=O
2050 RETURN
3000 REM Print Total in T
3010 REM Changes T; Uses C,D
3020 T=C-D; 0=5
3030 PRINT T/100," POUNDS",T%100," PENCE"
3040 RETURN
Values are entered in pence, and entering zero will terminate the list
of credits or debits.
The two subroutines at 1000 and 2000 are strikingly similar, and
this suggests that it might be possible to dispense with one of them.
Indeed, the main part of the chequebook-balancing program can be
written as follows, eliminating subroutine 1000:
10 REM Chequebook-Balancing Program
20 PRINT "ENTER CREDITS"
30 GOSUB 2000
40 C=D
50 PRINT "ENTER DEBITS"
60 GOSUB 2000
70 PRINT "TOTAL IS"
80 GOSUB 3000
90 END
In conclusion, subroutines have two important uses:
1. To divide programs into modules that can be written and tested
separately, thereby making it easier to understand the operation of
the program.
2. To make it possible to use the same piece of program for a number
of similar, related, functions.
As a rough guide, if a program is too long to fit onto the screen of
the VDU it should be broken down into subroutines. Each subroutine
should state clearly, in REM statements at the start of the
subroutine, the purpose of the subroutine, which variables are used by
the subroutine, and which variables are altered by the subroutine. A
few moments spent documenting the operation of the subroutine in this
_40_
way will save hours spent at a later date trying to debug a program
which uses the subroutine.
6.2 GOSUB Label
The GOSUB statement is just like the GOTO statement that has already
been described, in that it can be followed by a line number, an
expession evaluating to a line number, or a label. Labels are of the
form a to z, and the first line of the subroutine should contain the
label immediately following the line number.
6.2.1 Linear Interpolation
The following program uses linear interpolation to find the roots of
an equation using only integer arithmetic, although the program could
be modified to use floating-point statements.
The equation is specified in a subroutine, y, giving Y in terms of
X; the program finds solutions for Y=O.
As given, the program finds the root of the equation:
x2 - x - 1 = 0
The larger root of this equation is phi, the golden ratio. A scaling
factor of S=1000 is included in the equation so that calculations can
be performed to three decimal places.
The program prompts for two values of X which lie either side of
the root required.
1 REM Linear Interpolation
5 S=1000; 0=0; I=1
10 INPUT "X1",A,"X2",B
20 A=A*S; B=B*S
30 X=A; GOSUB y; C=Y
40 X=B; GOSUB y; D=Y
50 IF C*D<0 goto 80
60 print "root not bracketed"
70 end
80 do i="I+1
90" x="B-(B-A)*D/(D-C); GOSUB y
100 IF C*Y<0 THEN" a="X;" c="Y; GOTO 120
110" b="X;" d="Y
120 UNTIL ABS(A-B)<2 OR ABS(Y)<2
130 PRINTROOT IS" x="140 IF X<0 PRINT -
145 PRINT ABS(X)/S,.
150 DO" x="ABS(X)%S;" s="S/10
155 PRINT X/S; UNTIL" s="1
160 PRINT'NEEDED ,I, ITERATIONS.'
170" end
200yy="X*X/S-X-1*S
210 RETURN
Description of Program:
5-70 Check that starting values bracket a root
80-120 Find root by successive approximation
130-145 Print integer part of root
150-155 Print decimal places
160 Print number of iterations needed
200-210 y: Subroutine giving Y in terms of X, with appropriate
scaling.
_41_
Variables:
A - Lower starting value of X
B - Upper starting value of X
C - Value of Y for X=A
D - Value of Y for X=B
I - Iteration number
S - Scaling factor; all numbers are multiplied by S and held as
integers.
X - Root being approximated
Y - Value of equation for given,X
Program size - 466 bytes Sample run:
>RUN
X1?1
X2?3
ROOT IS X= 1.618
NEEDED 7 ITERATIONS.
6.3 Subroutines Calling Subroutines
Often the task carried out by a subroutine may itself usefully be
broken down into a number of smaller steps, and so it might be
convenient to include calls to subroutines within other subroutines.
This is perfectly legal, and subroutines may be nested up to a maximum
depth of 15 calls.
6.4 Recursive Subroutine Calls
Sometimes a problem can be more simply expressed if it is allowed to
include a reference to itself. When a subroutine includes a call to
itself in this way it is known as a 'recursive' subroutine call, and
it is possible to use recursive calls in ATOM BASIC provided that the
depth of recursion is limited to 15 calls. The following half-hearted
program uses a recursive call to print out ten stars without using a
loop:
10 REM Recursive Stars
20 P=10; GOSUB p
30 END
100pREN Print P stars
110 IF P=O RETURN
120 P=P-1
130 GOSUB p; REM Print P-1 stars
140 PRINT "*"
150 RETURN
This program could, of course, be written more effectively using a
simple FOR...NEXT loop. The following programs, however, use recursion
to great benefit to solve mathematical problems that would be much
harder to solve using iteration alone.
6.4.1 Tower of Hanoi Problem
In the Tower of Hanoi problem three pegs are fastened to a stand, and
there are a number of wooden discs each with a hole at its centre. The
discs are all of different diameters, and they all start on one peg,
arranged in order of size with the largest disc at the bottom of the
pile.
The problem is to shift the pile to another peg by transferring
_42_
one disc at a time, with the restriction that no disc may be placed on
top of a smaller disc. The number of moves required rises rapidly with
the number of discs used; the problem was classically described with
64 discs, and moving one disc per second the solution of this problem
would take more than 500,000 million years!
A recursive solution to the problem, stated in words, is:
To move F discs from peg A to peg B:
1. Move F-1 discs to peg C.
2. Move bottom disc to peg B.
3. Move F-1 discs to peg B.
Also, when F is zero there is no need to do anything. Steps 1 and 3 of
the procedure contain a reference to the whole procedure, so the
solution is recursive.
The following program will solve the problem for up to 13 discs,
and displays the piles of discs at every stage in the solution:
1 REM Tower of Hanoi
10 PRINT$12
20 A=TOP;D=A+4
40 V=-3;W=-1
60 !D=$1020300;!A=0
70 INPUT"NUMBER OF DISCS "F
80 A?1=F;?D=F 85 N=64/3
90 CLEARO
100 FORQ=1TOF;MOVE(F-Q),(2*(F-Q));PLOTlg(2*Q-1),0;NEXT
110 GOSUBh;END
1000hIF?D=O RETURN
1010 D!4=!D-1;D?6=D?1;D?5=D?2;D=D+4;GOSUBh
1020 MOVE(F-D?-4+D?V*N-N),(D?V?A*2);PLOT1,(D?-4*2-1),0
1030 MOVE(D?W*N-N),(D?W?A*2-2);PLOT3,(F+D?-4),0
1040 A?(D?W)=A?(D?W)+W;A?(D?V)=A?(D?V)-W
1050 D?3=D?-2;D?2=D?W;D?1=D?V;GOSUBh
1060 D=D-4;RETURN
Description of Program:
100 Draw starting pile of discs
110 Subroutine h is called recursively to move the number of
discs specified in ?D.
1000 h: Subroutine to move ?D discs
1010 Recursive call to move ?D-1 discs
1020 Draw new disc on screen
1030 Remove old disc from screen
1040 Set up array A
1050 Recursive call to put back ?D-1 discs
Variables: A?N - Number of discs on pile N
D - Stack pointer
?D - How many discs to transfer
D?1 - Destination Pile
D?2 - Intermediate pile
D?3 - Source pile
F - Total number of discs
N - One third of screen width
V - Constant
W - Constant
Program size: 461 bytes
Stack usage: (4 * number of discs) bytes
_43_
6.3.2 Eight Queens Problem
A classical mathematical problem consists of placing eight queens on a
chessboard so that no queen attacks any other. The following program
find all possible solutions to the problem, and draws a diagram of the
board to show each solution as it is found. The program uses many
abbreviations to keep it small enough to fit on an unexpanded ATOM
(for a complete explanation of these abbreviations, see section 10.1):
1 REM Eight Queens
30 C=O;D=TOP;E=D+3;A=D+27;!D=O
60 0=0;GOS.t;P.$13"THERE ARE "C" SOLUTIONS"';END
100tIF?D=OFF C=C+1;GOTOd
110 ?A=(?D\D?1\3?2):#FF
120lIF?A=OR.
130 A?1=?A&-?A
140 ?E=?D\A?1;E?l=(D?1\A?1)*2;E?2=(D?2\A?1)/2
150 D=D+3;E=E+3;A=A+2;GOS.t;D=D-3;E=E-3;A=A-2
160 ?A=?A&(A?1:OFF);GOT01
200dCLEARO;FORZ=OT032S.4;MOVEO,Z;DRAW31,Z;MOVEZ,O;DRAWZ,32;N.
210 Q=o;forz=3t024step3;p=top?z-Q;s=-2;dos=s+4;p=p/2;untilp=0
220 Q=top?z;plot13,(2/3*4-2),s;n.;p.$30 C;R.
Description of Program:
30 Initialise array space. D is vector of attacks, ?D is row
attacks, D?1 is left diagonal attacks, D?2 is right diagonal
attacks.
60 Call recursive analyser and print answer.
100 t: Recursive analyser: if all rows attacked have found a
solution.
110 Calculate possible places to put new queen.
120 If no possible place, end this recursive attempt.
130 Find least significant bit in possible places to use as new
queen position.
140 Calculate new attacked values.
150 Recursive call of analyser.
160 Remove this position from possible position and see if done.
200 d: Have solution, display board matrix.
210 Plot pixels at positions of queens.
220 Print the solution number at screen top and end recursion.
Variables:
?A - Possible position; value of A changes
C - Solutions counter
?D - Row attacks; value of D changes
E - Holds D+3 to make program shorter
Program size: 440 bytes
Vectors:
30 bytes
Total storage: 470 bytes.
_44_
7 Arrays and Vectors
So far we have met just 26 variables, called A to Z. Suppose you
wanted to plot a graph showing the mean temperature for every month of
the year. You could, at a pinch, use the twelve letters A to L to
represent the mean temperatures, and read in the temperatures by
saying:
INPUT A,B,C,D,E,F,G,H,I,J,K,L
However there is a much better way. A mathematician might call the
list of temperatures by the names:
t1, t2, t3, ..... t12.
where the 'subscript', the number written below the- line, is the
number of the month in the year. This representation of the twelve
temperatures is much more meaningful than using twelve different
letters to stand for them, and there is no doubt about which symbol
represents the temperature of, for example, the third month.
A similar series of variables can be created in ATOM BASIC, and
these are called 'arrays'. Each array consists of an array
'identifier', or name, corresponding to the name 't' in the above
example, and a 'subscript'. On most computers there is no facility for
writing subscripts, so some other representation is used. Each member
of the array can act as a completely independent variable, capable of
holding a value just like the variables A to Z. The members of an
array are called the array 'elements'. The total number of possible
elements depends on how the array was set up; in the above example
there were twelve elements, with subscripts from 1 to 12.
In addition to the standard type of array, ATOM BASIC provides two
other types of array called 'byte vectors' and 'word vectors'. Byte
vectors are useful when only a small range of numbers are needed, and
they use less storage space than word arrays. Word vectors use the
same amount of storage as arrays, but can be manipulated in a more
flexible manner.
7.1 Arrays - AA to ZZ
The array in ATOM BASIC consists of a pair of identical letters
a followed by the subscript in brackets: for example, EE(3). Each
element in this type of array can contain numbers as large as the
simple variables A to Z, namely, between about -2000 million and 2000
million.
Before an array can be used space must be reserved for it by a
DIM, or 'dimension', statement which tells BASIC how large the array
- is to be. For example, to reserve space for an array called AA with
the five elements AA(0), AA(1), AA(2), AA(3), and AA(4), the statement
would be:
DIM AA(4)
The DIM statement allocates space for arrays starting at the first
free memory location after the program text. If this were the first
a DIM statement encountered in the program the element AA(0) would be at
_45_
TOP, above the program text:
| TOP: |
| ? |
? |
? |
? |
^
AA(0) |
^
AA(1) |
^
AA(2) |
^
AA(3) |
|
The question marks represent unspecified values, depending on what the
array contained when it was dimensioned. If now another array were
dimensioned with the statement:
DIM BB(3)
space for the array BB would be reserved immediately following on from
AA.
Array elements can appear in expressions, and be assigned to, just
like the simple variables A to Z. For example, to make the value of
AA(3) become 776 we would execute:
AA(3)=776
Then we could execute:
AA(1)=AA(3)*2
AA(0)=AA(3)-6
and so on. The resulting array would now be:
| TOP: |
| 770 |
1552 |
? |
776 |
? |
^
AA(0) |
^
AA(1) |
^
AA(2) |
^
AA(3) |
^
AA(4) |
|
There are two places in BASIC programs where array elements may
not be used; these are:
l. As the control variable in a FOR...NEXT loop.
2. In an INPUT statement.
In these two cases the simple variables, A to Z, must be used.
7.1.1 Histogram
The following program illustrates the use of arrays to plot a
histogram of the temperature over the twelve months of the year. The
temperatures, assumed to be in the range 0 to 100, are first entered
in and are stored in the array TT(1..12).
1 REM Histogram
10 DIM TT(12)
20 FOR 2=1 TO 12;INPUT K
30 TT(J)=K; NEXT J
40 PRINT $12; CLEAR 0; 0=5
50 MOVE 60,12; DRAW 12,12
60 DRAW 12,42
70 FOR N=11 TO 0 STEP -1
80 IF N=7 PRINT "TEMP."
90 IF N%2=0 PRINT N*10
100 PRINT';NEXT N
110 PRINT " JAN MAR MAY JUL SEP NOV"'
120 PRINT " FEB APR JUN AUG OCT DEC"'
130 PRINT " MONTH"'
_46_
140 FOR N=1 TO 12; J=11+4*N
150 MOVE J,12; DRAW J,(TT(N)*3/10+12)
160 NEXT N; END
Description of Program:
20-30 Input 12 values
40 Clear screen
50-60 Draw axes
70-100 Label vertical axis
110-130 Label horizontal axis
140-160 Plot histogram bars
Program size: 415 bytes
Array storage: 52 bytes
7.1.2 Sorting Program
The following program illustrates the use of arrays to sort a series
of numbers into ascending order. It uses a fairly efficient sorting
procedure known as the 'Shell' sort. The program, as written, reads in
20 numbers, calls a subroutine to sort the numbers into order, and
prints the sorted numbers out.
1 REM Sorting
5 DIM AA(20)
10 FOR N=1 TO 20; INPUT J
20 AA(N)=J; NEXT N
30 N=20; GOSUB s
40 FOR N=l TO 20; PRINT AA(N)'
50 NEXT N
60 END
100sM=N
110 DO M=(M+2)/3
120 FOR I=M+1 TO N
130 FOR J=I TO M+1 STEP -M
140 IF AA(J)>=AA(J-M) GOTO b
150 T=AA(J); AA(J)=AA(J-M); AA(J-M)=T
160 NEXT J
170b NEXT I
180 UNTIL M=l; RETURN
Description of Program:
5-20 Read in array of numbers
30 Call Shell sort
40-50 Print out sorted array
100-180 s: Shell sort subroutine
140-150 Swap elements which are out of order.
Variables:
AA(1..20) - Array to hold numbers
I,J - Loop counters
N - Number of elements in array AA
M - Subset step size
T - Temporary variable
Program size: 332 bytes
Array storage: 84 bytes
7.1.3 Arbitrary-Precision Arithmetic
The following program allows powers of two to be calculated to any
precision, given enough memory. As it stands the program will
calculate all the powers of 2 having less than 32 digits. The digits
_47_
are stored in an array AA, one digit per array element. Every power of
2 is obtained from the previous one by multiplying every element in
the array by 2, and propagating a carry when any element becomes more
than one digit.
5 REM Powers of Two
10 DIM AA(31)
20 0=1; P=O
30 AA(0)=1
40 FOR J=1 TO 31
50 AA(J)=0
60 NEXT J
70 DO J=31
80 DO J=J-1; UNTIL AA(J)<>0
85 PRINT'"2"" P "="
90 FOR K=J TO 0 STEP -1
94 PRINT AA(K)
96 NEXT K
110 C=O
120 FOR J=O TO 31
130 A=AA(J)*2+C
140 C=A/10
150 AA(J)=A%10
160 NEXT J
170 P=P+1
180 UNTIL AA(31)<>0
190 END
Description of Program:
40-60 Zero array of digits
80 Ignore leading zeros
85-96 Print power
110-160 Multiply current number by 2
180 Stop when array overflows.
Variables:
AA - Array of digits; one digit per element
C - Decimal carry from one digit to next
J - Digit counter
K - Digit counter
P - Power being evaluated
Program size: 356 bytes
Array usage: 124 bytes
Total memory: 480 bytes.
7.1.4 Digital Waveform Processing
The following program uses a 256-element array to store a waveform
which can be low-pass filtered, converted to a square wave, or printed
out.
1 REM Digital Waveform Processing
5 DIM AA(255)
10 H=2000
15 CLEAR4
23 GOS.s; GOS.q
25 Z=160; GOS.p
28 GOS.1
30 Z=96; GOS.p
32 GOS.s
34 Z=32; GOS.p
_48_
90 END
1000pREM Plot Waveform
1005 MOVE 0,96
1010 FOR N=O TO 255
1020 PLOT13,N,(Z+AA(N)/H)
1030 NEXT N
1040 RETURN
2000sREM Make Sine Wave
2010 S=O;C=40000
2020 FOR N=O TO 255
2030 AA(N)=-S
2040 C=C-S/10
2050 S=S+C/10
2060 NEXT N
2070 RETURN
3000qREM Make Square Wave
3010 FOR N=O TO 255
3020 IF AA(N)<=0 AA(N)=40000
3030 IF AA(N)<0 aa(n)="-40000
3035 NEXT N
3040 RETURN
4000lREM Low Pass Filter
4010" b="O
4020 FOR" n="O TO 255
4030" b="AA(N)*360/1000+B*697/1000
4040" aa(n)="B; NEXT N
4050 RETURN
Description of Program:
23 Calculate a square wave
25 Plot it at top of screen
28 Low-pass filter the square wave
30 Plot it in centre of screen
32 Calculate a sine wave
34 Plot it at bottom of screen
1000-1040 p: Plots waveform
2000-2070 s: Calculates a sine wave.
3000-3040 q: Squares-up the waveform
4000-4050 l: Low-pass filters the waveform
Variables:
AA(0...255) - Array of points, values between -40000 and 40000.
B - Previous value for low-pass filter
C - Cosine of waveform
H - Scalinq factor for plotting waveforms
N - Counter
S - Sine of waveform
Z - Vertical coordinate for centre of waveform.
Program size: 564 bytes.
Array storage: 1024 bytes
Total memory: 1588 bytes
_49_
Sample plot:
7.1.5 Subscript Checking
Many BASIC interpreters perform extensive checking whenever an array
element is used in a program. For example, if an array were
dimensioned:
DIM RR(10)
then every time the array were used the subscript would be checked to
make sure that it was both 0 or greater, and 10 or less. Obviously
these two checks slow down the execution of a program, and so in ATOM
BASIC only the first check is performed, so that only positive
subscripts are allowed. It is left to the programmer to ensure that
subscripts do not go out of range. Assigning to an array whose
subscript is out of range will change the values of other arrays, or
strings, dimensioned after that array.
If required, the programmer can easily add array subscript
checking; for example, if the array assignment were:
RR(A)=35
the statement:
IF A>10 THEN ERROR
could be added before the assignment to cause an error if the array
subscript, A, went out of range.
7.1.6 Multi-Dimensional Arrays
The standard types of array in ATOM BASIC are one-dimensional. In
other words, they have just one subscript, and so can be visualised as
lying in a straight line; hence the name 'array'.
Sometimes it is convenient to make each element of an array
represent a cell in a square 'matrix'; each element would then have
two subscripts corresponding to the column and row of that square.
Such two-dimensional arrays are called 'matrices'. Consider the
following representation of a 3 by 6 matrix:
_50_
The whole matrix has 3 x 6 = 18 elements, and the element shown with
an X would have the subscripts (2,4).
ATOM BASIC does not have a direct representation for
two-dimensional (or higher dimension) arrays, but they are easily
represented using the single-dimension arrays AA to ZZ as described in
the following sections.
7.1.7 Calculation of Subscripts
To represent a two-dimensional matrix using a one-dimensional array
imagine the matrix divided into rows as shown:
The first element of row 1, with subscripts (1,0), follows immediately
after the last element of row 0, with coordinates (0,5). Consider the
general case where the matrix has M rows numbered 0 to N-l, and N
columns numbered 0 to N-1. The matrix can be dimensioned, using a
one-dimensional array, with the DIM statement:
DIM XX(M*N-1)
Any array element, with subscripts A and B, can be referenced as:
XX(A*N+B)
In the earlier example the array had dimensions 3 x 6 and so would be
dimensioned:
DIM XX(17)
The array element with subscripts (2,4) would be given by: xx(16)
7.1.8 Solving Simultaneous Equations
The following program will solve a number of linear simultaneous
equations, using a matrix to hold the coefficients of the equations,
and a matrix inversion technique to find the solution. The program
prints the solutions as integers, where possible, or as exact
fractions.
This method has the advantage over the standard pivotal
condensation technique that for integer coefficients the answers are
exact integers or fractions.
The example run shown solves the pair of equations:
a + 2b + 1 = 0
4a + 5b + 2 = 0
10 REM Simultaneous Equations
50 INPUT"NUMBER OF EQUATIONS="N
60 I=N*N;J=N*(N+1)
_51_
65 DIM AA(I),CC(J),II(N)
70 0=0;FOR I=1TON;FOR J=1TO N+1
80 PRINT"C("I","J")=";INPUT C
90 CC((I-1)*(N+1)+J)=C;NEXT J;NEXT I
100 L=N+1;GOSUB c;E=D;M=l-2*(N%2)
110 PRINT'"SOLUTION:"'
112 IF E<0 e="-E;M=-M
115 IF" e="O;PRINTDEGENERATE!';END
120 FOR" l="1TON;GOSUB c
125" print"x("l")="130" a="M*D;B=E;DO" a="A%B
140 IF ABS(B)">ABS(A) THEN T=B;B=A;A=T
150 UNTIL B=O;A=ABS(A)
151 P.(M*D)/A;IF E/A<<1 PRINT"/"E/A
155 M=-M;PRINT';NEXT L;END
160cFOR I=1TON;FOR J=1TON;K=I*N-N+J
170 IF J<l aa(k)="CC(K+I-1)
180 IF J"<=L AA(K)=CC(K+I)
190 NEXT J;NEXT I
200dD=O;F=l;S=l
210 FOR J=1TON;II(J)=J;F=F*J;NEXT J
215 GOSUB f
220 FOR H=2TOF;GOSUB e;NEXT H;RETURN
230eI=N-1;J=N
240gIF II(I)>=II(I+1) I=I-1;GOTO g
250hIF II(I)>=II(J) J=J-1;GOTO h
260 GOSUB i;I=I+1;J=N;IF I=J GOTO f
270 DO GOSUB i;I=I+1;J=J-1;UNTIL I>=J
280fp=i;FOR K=1TON;P=P*AA(N*K-N+II(K))
290 NEXT K;D=D+S*P;RETURN
300iK=II(I);II(I)=II(J);II(J)=K
310 S=-S;RETURN
Description of Program:
50-60 Allocate space for matrix
70-90 Read in matrix of coefficients
120-155 Print solutions
130-150 Find GCD of solution, so it is printed in lowest terms
160-190 c: Permute terms to obtain next addition to determinant; i.e.
for 5 equations, starting with (1,2,3,4,5) run through all
permutations to (5,4,3,2,1).
280-290 f: Add in next product to determinant.
300-310 i: Swap terms in permutation.
Variables:
AA(1...N*N) - Matrix
CC(1...N*N+N) - Matrix of coefficients
S - Signature of permutation.
Program Size: 932 bytes.
Variable Space: (2*(N*N+N)+3)*4 bytes
Sample run:
<RUN
NUMBER OF EQUATIONS=?2
C(1,1)=?1
C(1,2)=?2
C(1,3)=?1
C(2,1)=?4
C(2,2)=?5
C(2,3)=?2
_52_
SOLUTION:
X(1)= 1/3
X(2)= -2/3
7.2 Byte Vectors Using, '?'
It is sometimes wasteful of memory to allocate space for numbers over
the range provided by word arrays so a second type of array
representation is provided which only allocates one byte, rather than
four bytes, for each array element. These are referred to as 'byte
vectors', and they are in effect one-dimensional arrays. Byte vectors
differ from word arrays in that they use one of the simple variables A
to Z to hold the 'base' address of the array; i.e. the address in
memory where the zeroth element of the array will reside. The array
subscripts are simply 'offsets' from this base address; i.e. the
subscript is added to the base address to give the address of the
array element. The vector elements are written as:
A?0, A?1, A?2, ... etc
where A is the simple variable used to hold the base address of the
vector, and the number following the question mark is the subscript.
Note that the zeroth element of a byte vector, A?0, is equivalent
to ?A, the contents of the location with address A. Similarly A?1 is
equivalent to ?(A+1), and so on.
Byte vectors can be dimensioned by the DIM statement; for example,
to dimension a byte vector with elements from A?0 to A?11 the
statement would be:
DIM A(11)
Because the DIM statement dimensions arrays and vectors from the end
of the program onwards, the above DIM statement is equivalent to:
T=ZOP; A=T; T=T+12
where T is a variable used to keep track of the next free memory
location. Note that space for vectors can be reserved anywhere in
memory, as distinct from arrays which can only be assigned from TOP
onwards using the DIM statement. For example, to assign space for a
vector S corresponding to the screen memory, simply execute:
S=#8000
Elements of this vector would then correspond to locations on the
screen; e.g. S?31 is the location corresponding to the top right-hand
corner of the screen.
Each element of a byte array can hold a positive number between 0
and 255, or a single character. Strings are simply byte vectors
containing characters. Note that the subscript of a byte array can be
an arbitrary expression provided that it is enclosed in brackets.
7.3 Word Vectors Using '!'
A second representation for word arrays is provided in ATOM BASIC
using the word indirection operator '!', and is mentioned here for
completeness, although for simple problems involving arrays the word
arrays AA to ZZ are probably more convenient. Word vectors are similar
to the byte vectors already described, but each element of the vector
consists of a word rather than a byte. Each element consists of the
base address variable separated from the subscript, or offset, by a
'pling' '!'. Note that the subscript should be incremented by 4 for
each element, since each element is offset 4 bytes from the previous
one. For example, a word vector W might have the six elements:
_53_
W!O, W!4, W!8, W!12, W!l6, W!20.
Space can be dimensioned for word vectors by using the DIM statement,
and allowing 4 bytes per element; for example, to provide storage for
the above 6 elements, execute:
DIM W(23)
Note that the zeroth element of the vector, W!0, is equivalent to !W.
7.3.1 Prime Numbers
The following program finds all the prime numbers up to 99999. It uses
a word vector to store primes already found, and only tests new
candidates for divisibility by these numbers:
1 REM Prime Numbers
10 @=8;S=4;Z=O;J=TOP;G=J;!G=3;PW+S
20 FORT=3T099999STEP2
30cIFT%!G=Z G=J;N.
40 IFT>!G*!G G=G+S;G.c
50 P.T;!P=T;G=J;P=P+S;N.
60 END
Description of Program:
10 Set up vector
20 Test all odd numbers
30 If divisible, try another.
40 Have we tried enough divisors?
50 Must be prime - print it.
Variables:
!G - Divisor being tested
J - Equal to TOP
!P - Vector of divisors
S - Bytes per word
T - Candidate for prime
Z - Constant zero.
Program size: 155 bytes
Vector: as required.
7.3.2 Call by Reference
A major advantage of word vectors over the word arrays is that their
base addresses are available as values, and so can be passed to
subroutines. As an example, consider this program:
10 A=TOP; B=A+40
.
.
90 P=A; GOSUB p; REM Output A
94 P=B; GOSUB p; REM Output B
98 END
100pREM Print 10 Elements of array P
105 @=8; PRINT I
110 FOR J=O TO 39 STEP 4
120 PRINT P!J
130 NEXT J
140 PRINT '
150 RETURN
_54_
In this example subroutine p can be used ta print any array by passing
its base address over in the variable P; this is known as a 'call by
reference' because the subroutine is given a reference to the array,
rather than the actual values in the array.
7.3.3 Arbitrary Precision Powers
The following program illustrates the use of word vectors to calculate
the value of any number raised to any other number exactly, limited
only by the amount of memory available. The program stores four
decimal digits per word, so that the product of two words will not
cause overflow, and the result is calculated as a word vector.
1 REM Arbitrary Precision Powers
5 T=#3BFF
10 H=(T-TOP)/3; DIM P(H),S(H),D(H)
15 H=10000
20 @=0;PRINT'" POWER PROGRAM"
30 PRINT'" COMPUTES Y X, WHERE x>0 AND Y>0"
40 INPUT'" VALUE OF Y"Y," VALUE OF X"X
50 IFX<10ry<1print” value out of range";run
60 n="Y;N=X;GOSUBp
70 PRINT Y" "x"="P!!P;IF!P<8 RUN
90" f.l="!P-4T04STEP-4
95 IFL!P<1000P.O
100 IFL!P<100P.O
110 IFL!P<10P.O
120" p.l!p;n.;run
140*
200pj="M;IFN%2=0J=1
210" r="P;GOS.e;J=M;R=S;GOS.e;IFN=1R.
250" b="S;DOA¿B;GOS.m;B=E
255" n="N/2;A=P;IFN%2GOS.m;P=E
260" u.n<2;r.
280*
300mld="IA+lB+4;F.J=4TOID+4S.4
310 D!J¿O;N.;W¿D-4
320 F.J¿4TO!B" s.4;c="O;G=BlJ
325" v="W+J;F.L¿4TO!A S.4
330" q¿a!l*g+c+v!l;v!l="q%h
340" c="Q/H;N.;V!LW;N.
370 DO!DE!0-4;U.D!!DC">0;E=D;D=A;R.
380*
400e!R=O;DO!R=lR+4;R!lR=J%H
410 JW/H;U.J<1;r.
description of program:
5 set t to top of lower text space.
10 divide available memory between p, s, and d
20-40 read in values of y and x
50 disallow negative values
60 calculate power
70 print result if fits in one word
90 print rest of result, filling in leadinq zeros.
140 blank line to make listing clearer.
200-260 p: calculates power. looks at binary representation of x and
for each bit squares b, and if bit is a 1 multiplies p by
current b.
300-370 m: multiply together the vectors pointed to by a and b and
put the result into the vector pointed to by d. pointers to
vectors get changed; e points to result.
_55_
400-410 e: Unpack J into vector pointed to by R; store number of
words in !R.
Variables:
D!0... - Workspace vector
H - Radix for arithmetic
P!1... - Vector for unpacked result
!P - Number of elements used in P
S!0... - Workspace vector
T - Top of available memory
Program size: 733 bytes.
Additional storage: as available.
Sample run:
>RUN
POWER PROGRAM
COMPUTES Y"X, WHERE X>0 AND Y>0
VALUE OF Y?16
VALUE OF X?64
16^64=1157920892373161954235709850086879078532699846656405640394575
84007913129639936
7.3.4 Vectors of Vectors
A second way of representing two-dimensional arrays is possible using
the ATOM's indirection operators '?' and '!'; this avoids the need for
a multiplication to calculate the subscript, but does require slightly
more storage. The idea is to think of a two-dimensional matrix as a
vector of vectors; first a vector is created containing the addresses
of the rows of the matrix. For example, for a matrix called X with
columns 0 to M, and rows 0 to N, the following statements will set up
the vector of row addresses:
DIM X(2*N-1)
FOR J=O TO N*2 STEP 2; DIM Q(m); X!J=Q; NEXT J
A word array is used to hold the base addresses. Q is a variable used
to hold the base address temporarily. Now that the vector of row base
addresses has been set up, the element with subscripts A,B is:
X!(A*2)?B
_56_
8 strings
A 'string' is a sequence of characters; the characters can be anything
letters, digits, or punctuation marks. They can even be control
characters.
8.1 Quoted Strings
Strings are represented in a program by enclosinq the characters
between quotation marks; quoted strings have already been introduced
in the context of the PRINT and INPUT statements. For example:
"THIS IS A STRING"
To represent a quotation mark in a quoted string the quotation mark is
typed twice. Valid strings always contain an even number of quotation
marks. For example:
PRINT"HE SAID: ""THIS IS A VALID STRING"""
will print:
HE SAID: "THIS IS A VALID STRING"
8.2 String Variables
The variables A to Z have already been met, where they are used to
represent numbers. These variables can also be used to represent
strings, and strings can be manipulated, input with the INPUT
statement, printed with the PRINT statement, and there are several
functions for manipulating strings.
8.2.1 Allocating Space for Strings
BASIC allows strings of any size up to 255 characters. To use string
variables space for the strings should first be allocated by means of
a DIM (dimension) statement. For example, for a string of up to 10
characters using the variable A the statement would be:
DIM A(10)
Any number of strings can be dimensioned in one DIM statement.
8.2.2 String Operator '$'
Having allocated space for the string it can then be assigned a value.
For example:
$A="A STRING"
The '$' is the string-address operator. It specifies that the value
following it is the address of the first character of a string.
The effect of the statement DIM A(10) is to reserve 11 memory
locations in the area of free memory above the text of the BASIC
program, and to put the address of the first of those locations into
A. In other words, A is a pointer to that area of memory. After the
above assignment the contents of those locations are as follows:
_57_
The question-marks indicate that the last two locations could contain
anything. The character ' ' represents 'return' which is automatically
stored in memory to indicate the end of the string. The DIM statement
allocates one extra location to hold this terminator character,
although you will not normally be aware of its presence.
Note that it would be dangerous to allocate a string of more than
10 characters to A since it would exceed the space allocated to A.
8.2.3 Printing strings
A string variable can be printed by writing:
PRINT $A
This would print:
A STRING>
and no extra spaces are inserted before or after the string.
8.2.4 String Assignment
Suppose that a second string is dimensioned as follows:
DIM B(8)
The string $A can be assigned to $B by the statement:
$B=SA
which should be read as 'string B becomes string A'. The result of
this assignment in memory is as follows:
| A: |
| A |
|
S |
T |
R |
I |
N |
G |
~ |
? |
? |
A |
|
S |
T |
R |
I |
N |
G |
~ |
^
A |
|
|
|
|
|
|
|
|
|
|
^
B |
|
|
|
|
|
|
|
|
|
8.2.5 String Equality
It is possible to test whether two strings are equal with the IF
statement. For example:
$A="CAT"; $B="CAT"
IF $A=$B PRINT "SAME"
would print SAME.
8.2.6 Strinq Input
The INPUT statement may specify a string variable, in which case the
string typed after the '?' prompt, and up to the ’return', will be
assigned to the string variable. The maximum length of line that can
be typed in to an INPUT statement is 64 characters so, for safety, the
string variable in the INPUT statement should be dimensioned with a
length of 64.
8.3 String Functions
Several functions are provided to help with the mainpulation of
strings.
_58_
8.3.1 Length of a String - LEN
The LEN function will return the number of characters in the string
specified in its argument. For example:
$A="A STRING"
PRINT LEN(A)
will print the value 8. Note that:
$B=""""
PRINT LEN(B)
will print 1 since the string B contains only a single quote
character.
8.3.2 CH
The CH function will return the ASCII value of the first character in
the string specified by its argument. Thus:
CH"A"
will be equal to 65, the ASCII code for A. The string terminating
character 'return' has a value of 13, so:
CH""
will be equal to 13.
8.4 String Manipulations
The following sections show how the characters within strings can be
manipulated, and how strings can be concatenated into longer strings
or broken down into substrings.
8.4.1 Character Extraction - '?'
Individual Characters in a string can be accessed with the
question-mark ’?' operator. Consider again the representation of the
string A. Number the characters, starting with zero:
| |
| A |
|
S |
T |
R |
I |
N |
G |
~ |
? |
? |
0
^
A |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
The value of the Nth. character in the string is then simply A?N. For
example, A?7 is "G", etc. In general A?B is the value of the character
stored in the location whose address is A+B; therefore A?B is
identical to B?A. In other words, a string is being thought of as a
byte vector whose elements contain characters; see section 7.2.
The following program illustrates the use of the '?’ operator to
invert all the characters in a string which is typed in:
1 REM Invert String
5 DIM Q(64)
10 INPUT $Q
20 FOR N=O TO LEN(Q)-1
30 Q?n=q?n fg 020
40 NEXT N
50 PRINT $Q
60 RUN
_59_
8.4.2 Encoding/Decoding Program
As a slightly more advanced example of string operations using the ’?'
operator, the following program will produce a very secure encoding of
a message. The program is given a number, which is used to 'seed'
BASIC's random number generator. To decode the text the negative of
the same seed must be entered.
1 REM Encoder/Decoder
10 S=TOP; ?12=0
20 INPUT'"CODE NUMBER"T
30 !8=ABS(T)
40 INPUT'$S
50 FOR P=S TO S+LEN(S)
60 IF ?P<041 goto 100
70 r="ABS(RND)%26
80 IF T<0 THEN" r="26-R
90" ?p="(?P-041+R)%26+#41 100 NEXT P
110 PRINT $S
120 GOTO 40
Description of Program:
20 Input code number
30 Use code nurrber to seed random number generator
40 Read in line of text
50-100 For each cl aracter, if it is a letter add the next random
number to it, modulo 26.
110 Print out encoded string.
Variables:
P - Address of character in string
R - Next random number
S - Address of string; set to TOP.
T - Code number
Program size:
String storage: up to 64 bytes
Sample run:">RUN
CODE NUMBER?123
?MEETING IN LONDON ON THURSDAY BGYKPYI CM NHSHVO VU RGFGDHJI
<RUN
CODE NUMBER?123
? MEETING IN LONDON ON THURSDAY
BGYKPYI CM NHSHVO VU RGFGDHJI
? <
<RUN
To illustrate how secure this encoding algorithm is you may like to
attempt to find the correct decoding of the following quotation:
YUVHW ZY WKQN IAVUAG Qm SHXTSDK
GSY IEJB RZTNOL UFQ FTONB JB BY
CXRK Qcjf UN TJRB.
SWB FJA IYT WCC LQFWHA YHW OHRMNI OUJ
_60_
HTJ I TYCU GQYFT FT SGGHH HJ FRP ELPHQMD,
RW LN Qohd OQXSER CUAB.
DKLCLDBCV.
8.4.3 Concatenation
Concatenation is the operation of joining two strings together to make
one string. To concatenate string B to the end of string A execute:
$A+LEN(A)=$B
For example:
10 DIM A(10),B(5)
20 $A="ATOM"
30 $B="BASIC"
40 $A+LEN(A)=$B
50 PRINT $A
60 END
will print:
ATOMBASIC>
8.4.4 Right-String Extraction
The right-hand part of a string A, starting at character N, is simply:
$A+N
For example, executing:
10 DIM A(10),B(5)
20 $A="ATOMBASIC"
30 $B=$A+4
40 END
will give string B the value "BASIC".
8.4.5 Left-String Extraction
A string A can be shortened to the first N characters by executing:
$A+N=""
Since the 'return' character has the value 13, this is equivalent to:
A?N=13
8.4.6 Mid-String Extraction
The middle section of a string can be extracted by combining the
techniques of the previous two sections. For example, the string
consisting of characters M to N of string A is obtained by:
$A+N=""; $A=$A+M
For example:, if the following is executed:
10 DIM A(10)
20 $A="ATOMBASIC"
30 $A+5=0"; $A=SA+1
40 END
then string A will have the value "TOMB".
_61_
8.5 Arrays of Fixed-Length Strings
The arrays AA to ZZ may be used as string variables, thus providing
the ability to have arrays of strings. To allocate space for an array
of strings the DIM statement can be incorporated into a FOR...NEXT
loop. For example, the followinq program allocates space for 21
strings, AA(0) to AA(20), each capable of holding 10 characters:
25 DIM AA(20)
35 FOR N=O TO 20
40 DIM J(10)
50 AA(N)=J
60 NEXT N
Note the use of a dummy variable J to allocate the space for each
string. Individual elements of the string array can then be assigned
to as follows:
$AA(0)="ZERO"
$AA(10)="TEN"
and so on.
8.5.1 Day of Week
The following program calculates the day of the week for any date in
the 20th. century. It stores the names of the days of the week in a
string array.
1 REM Day of Week
10 DIM AA(6)
20 FOR N=O TO 6; DIM B(10); AA(N)=B; NEXT N
30 $AA(0)="SUNDAY”; $AA(1)=”MONDAY"
40 Saa(2)="tuesday";$aa(3)="wednesday"
50 $AA(4)="THURSDAY";$AA(5)="FRIDAY"
60 $AA(6)="SATURDAY"
70 INPUT"DAY OF WEEK"'’"YEAR "Y,"MONTH ”M,"DATE IN MONTH "D
80 Y=Y-1900
90 IF Y<0 or y<99 PRINT"ONLY 20TH CENTURY I"';GOTO 70
100 IF M>2 THEN M=M-2; GOTO 120
110 Y=Y-1; M=M+10
120 E=(26¿M-2)/10+D+Y+Y/4+19/4-2*19
130 PRINT"IT IS "$AA(ABS(E%7))
140 END
Description of Program:
10-20 Allocate space for string array 30-60 Set array elements
70 Input date
80-120 Calculate day
130 Print day of week.
Variables:
$AA(0...6) - String array to hold names of days
B - Temporary variable to hold base address of each string
D - Date in month
E - Expression which, modulo 7, gives day of week.
M - Month
N - Counter
Y - Year in 20th. century.
Program size: 458 bytes.
Array storage: 105 bytes.
_62_
Total memory: 563 bytes.
8.6 Arrays of Variable-Length Strings
The most economical way to use the memory available is to allocate
only as much space as is needed for each string. For example the
following program reads in 10 strings and saves them in strings called
VV(1) to VV(10):
10 DIM VV(10),T(-1)
20 FOR N=1 TO 10
30 INPUT $T
40 VV(N)=T
50 T=T+LEN(T)+1
60 NEXT N
70 INPUT "STRING NUMBER",N
80 PRINT $VV(N),'
90 GOTO 70
The statement DIM T{-1) sets T to the address of the first free memory
location. T is then incremented past each string to the next free
memory location as each string is read in. Finally, when 10 strings
have been read in the program prompts for a string number and types
out the string of that number.
For example, if the first three strings entered were: "ONE",
"TWO", and "THREE”, the contents of memory would be:
| |
| O |
N |
E |
~ |
T |
W |
O |
~ |
T |
H |
R |
E |
E |
~ |
? |
? |
? |
^
VV(1) |
^
VV(2) |
^
VV3 |
^
T |
|
8.7 Reading Text
Some BASICs have statements READ and DATA whereby strings listed in
the DATA statements can be read into a string variable using the READ
statement.
Although ATOM BASIC does not provide these actual statements,
reading strings specified as text is a fairly simple matter. The
following program reads the strings "ONE", "TWO" ... etc. into a
string variable, $A, and prints them out. The strings for the numbers
are specified as text after the program. They are identified by a
label 't', and a call to subroutine 'f' sets Q to the address of the
first string. Subroutine 'r' will then read the next string from the
list:
10 REM Read Text
20 DIM A(40); L=CH"t"
25 GOSUB f
30 FOR J=l TO 20; GOSUB r
40 PRINT $A
50 NEXT J
60 END
500fREM point Q to text
510 Q=218*256
520 DO Q=Q+1
530 UNTIL ?Q=0d AND Q?3=l
540 Q=Q+4; RETURN
550*
600rREM read next entry into A
_63_
605 REM changes: A,Q,R
610 R=-1
620 DO R=R+1; A?R=Q?R
630 UNTIL A?R=CH"," OR A?R=0D 640 IF A?R=fD Q=Q+3
650 Q=Q+R+1; A?R=0D; RETURN
660*
800tONE,TWO,THREE,FOUR,FIVE
810 SIX,SEVEN,EIGHT,NINE,TEN
820 ELEVEN,TWELVE,THIRTEEN
830 FOURTEEN,FIFTEEN,SIXTEEN
840 SEVENTEEN,EIGHTEEN,NINETEEN
850 TWENTY
Description of Program:
25 Find the text
30 Read in the next string
40 Print it out
500-550 f.: Search for label t and point Q to first string
600-660 r: Read up to comma or return and put string into $A
800-850 t: List of 20 strings
Variables:
$A - String
J - Counter
L - Label for text
Q - Pointer to strings
R - Temporary pointer
Program size: 511 bytes
String storage: 41 bytes
Total memory: 552 bytes.
The program can be moaified to read from several different blocks of
text with different labels by changing the value of L. Also note that
the character delimiting the strings may be any character, specified
in the CH function in line 630.
8.7.1 Reading Numeric Data
Numeric data can be specified as strings of characters as in in the
Read Text program of the previous section, and converted to numbers
using the VAL command in the extension ROM. For example, modify the
Read Text program by changing line 40 to:
40 FPRINT VAL A
and provide numeric data at the label 't', for example as follows:
800t1,2,3,4,1E30,27,66
810 91,1.2,1.3,1.4,1.5
820 13,14,15,16,17
830 18,19,20
8.8 Printing Single Characters - '$'
A special use of the '$' operator in the PRINT statement is to print
characters that can not conveniently be specified as a string in the
program, such as control characters and graphics symbols. Normally '$’
is followed by a variable used as the base address of the string. If,
however, the value following the dollar is less than 255, the
character corresponding to that code will be printed instead.
The following table gives the control codes, characters, and
graphics symbols corresponding to the different codes:
_64_
Hex: Decimal: Character Printed:
#00 - #1F 0 - 31 Control codes
#20 - 05F 32 - 95 ASCII cnaracters
#60 - #9F 96 - 159 Inverted ASCII characters
#A0 - #DF 160 - 223 Grey graphics symbols
4EO - #FF 224 - 255 White graphics symbols
Note that only half of the 64 possible white graphics symbols can be
obtained in this way.
The most useful control codes are specified in the following
sections; for a full list of control codes see section 18.1.3.
8.8.1 Cursor Movement
The cursor can be moved in any of the four directions on the screen
using the following codes:
Hex: Decimal: Cursor Movement:
#08 8 Left
#09 9 Right
#OA 10 Down
#Os 11 Up
The screen is scrolled when the cursor is moved off the bottom line of
the screen; the cursor cannot be moved off the top of the screen. Note
that the entire screen memory is modified by scrolling; every line is
shifted up one line, and the bottom line is filled with spaces.
8.8.2 Screen Control
The following control codes are useful for controlling the VDU screen:
Hex: Decimal: Control Character:
#OC 12 Clear screen and home cursor
#1E 30 Home cursor to top left of screen
8.8.3 Random Walk
The following program prints characters on the screen following a
random walk. One of the cursor control codes, chosen at random, is
printed to move the cursor; a white graphics character, chosen at
random, is then printed followed by a backspace to move the cursor
back to the character position.
1 REM Random Walk
10 DO
20 PRINT $ABS(RND)%4+8, $(0AO+ABS(RND)1#40), $8
30 UNTIL 0
_65_
_66_
9 Reading and Writing Data
The reader should now be familiar with the three types of data that
can be manipulated using ATOM BASIC, namely:
1. Words i.e. numbers between -2000 million and 2000 million
(approximately).
Storage required: 4 bytes
e.g. variables A to Z
arrays AA(1) ... etc.
word vectors A!4 ...etc.
indirection !A ...etc.
2. Bytes i.e. numbers between 0 and 255, or single characters, or
logical values.
Storage required: 1 byte
e.g. byte vectors A?1 ... etc.
indirection ?A ...etc.
3. Strings i.e. sequences of between 0 and 255 characters, followed by
a 'return'.
Storage required: Length+1 bytes
e.q. quoted string "A STRING"
string variable $A ...etc.
All these types of data can be written to cassette and read from
cassette, making it very simple to make files of data generated by
programs.
The ATOM BASIC functions and statements for cassette input and
output are designed to be fully compatible with the disk operating
system, should that be added at a later stage. When the disk operating
system is used, several files can be used by one program, and the
individual files are identified by a 'file handle', a number
specifying which file is being referred to. Although this facility is
not available when working with a cassette system, the file handle is
still required for compatibility.
9.2 Output
To output a word to cassette the PUT statement is used. Its form is:
PUT A,W
where A and W are the file handle, and word for output, respectively.
To output a byte to cassette the BPUT statement is used; the form 1S:
BPUT A,B
where A is the file handle, and B is the byte for output.
To output a string the SPUT statement is used. The form is:
SPUT A,S
where A is the file handle, and S is the base address of the string.
_67_
9.3 Input
To read a word from cassette the GET function is used. Its form is:
GET A
where A is the file handle. The function returns the value of the
word.
To read a byte the BGET function is used. Its form is:
BGET A
where A is the file handle. The BGET function returns the value of the
byte, and can therefore be used in expressions; for example:
PRINT BGET A + BGET A
will read two bytes from cassette and print their sum.
To read strings the SGET statement is used. The form is:
SGET A, S
where A is the file handle, and S is the base address where the string
will be stored. The string S should be large enough to accomodate the
string being read.
Note the difference between SGET, which is a statement, and the
functions BGET and GET; SGET cannot be used in expressions.
9.4 Find Input and Find Output
The functions FIN (find input) and FOUT (find output) can optionally
be called before inputting from, or outputting to, cassette. The
functions are called with a null string as the argument, and they
return the value 13; when used with a disk system the argument is the
file name, and the value returned is the file handle.
The FOUT function is called as follows:
A=FOUT""
and it will cause the message:
RECORD TAPE
to be printed, and the program will wait for a key to be pressed
before continuing execution.
The FIN function is called as follows:
A=FIN""
and it causes the message:
PLAY TAPE
to be printed, and again the program will wait for a key to be
pressed. A dummy variable, such as A in this example, should be used
to hold the file handle.
9.4.1 Data on Cassette
The following program prompts for a series of values, terminated by a
zero, and saves them on a cassette tape. The first byte saved on the
tape is the number of words of data saved.
1 REM Data to Cassette
10 DIM VV(20)
20 N=O
30 DO INPUT J
40 VV(N)=J; N=N+1
50 UNTIL J=O OR N>20
60 A=FOUT""
_68_
70 BPUT A,(N-1)
80 FOR M=O TO N-1
90 PUT A,VV(M) 100 NEXT M
110 END
Description of Program:
30-50 Input numbers
60 Warn user to start tape
70 Output number of bytes
80-100 Save values on cassette
Variables:
A - Dummy file handle
J - Temporary variable for values input
M - Counter
N - Counter for number of values
VV(0...20) - Array of numbers
The next program reads the values back in and plots a histogram of the
values. The program automatically scales the values if they are too
large to fit onto the screen.
1 REM Plot Histogram from Cassette
10 DIM VV(20)
20 A=FIN""; N=BGET A
30 FOR M=O TO N
4O VV(M)= GET A
50 NEXT M
60 REM X=Maximum, Y=Minimum
70 X=VV(0); Y=VV(0)
80 FOR M=1 TO N
90 IF X<vv(k) then x="VV(M)
100 IF Y"<VV(M) THEN Y-VV(M)
110 NEXT M
120 S=(X-Y+63)/64
130 REM Plot Histogram
135 CLEAR 0
140 FOR M=O TO N
150 MOVE O,M
160 DRAW ((VV(M)-Y)/S),M
170 NEXT M
180 GOTO 180
Description of Program:
20-50 Read values into array
70-110 Find maximum and minimum values in array
120 Calculate scaling factor
140-170 Plot scaled histogram
180 Wait for ESC key.
Variables:
A - Dummy file handle
M - Counter
N - Number of values in array
S - Scale factor for array
VV(0...20) - Array of values
X - Maximum value
Y - Minimum value
_69_
9.5 Reading and Writing Speed
When writing data to the cassette it is important to remember that the
program reading the data back will not be able to control the
cassette; it will have to read the data before it has passed under the
tape head. If the program to read the data will spend a substantial
time between reading, it may miss bytes passing under the tape head
unless a delay is inserted between bytes when writing to tape.
As a general guide, the program to read the data should take no
longer to read each byte than the program to write the data takes to
write it.
9.6 Animal Learning Program
The following program illustrates how a computer can be 'taught'
information, so that a 'database' of replies to questions can be built
up. The computer plays a game called 'Animals'; the human player
thinks of an animal and the computer tries to guess it by asking
questions to which the answer is either 'yes' or 'no'. Initially the
computer only knows about a dog and a crow, but as the game is played
the computer is taught about all the animals that it fails to guess.
The program uses the cassette input/output statements to load the
database, or tree, from cassette at the start of the game, and to save
the enlarged database at the end of the game.
First create a database by typing:
GOSUB 9000;
and record the database on a cassette. Then RUN the program and load
the database you have just recorded. When the reply ’NO’ is given to
the question 'ARE YOU THINKING OF AN ANIMAL' the program will save the
new, enlarged, database on cassette. Also given is a sample run which
was obtained after several new animals had been introduced to the
computer.
1 REM Animals
10 REM Load Tree
20 F=FIN""
23 DO UNTIL BGET F=#AA
25 FOR T=TOP TO TOP+GET F
30 ?T=BGET F; NEXT T
35 DO X=TOP
40 PRINT'"ARE YOU THINKING OF AN ANIMAL"
45 GOSUB q
48 IF Q=O THEN GOSUB z; END
50 DO PRINT $X+1
60 GOSUB q
65 P=X+LENX+1+Q; X=!P+TOP
70 UNTIL ?X<CH"*"
75 PRINT"IS IT "$X
80 GOSUB q
85 IF Q=4 PRINT "HO-HO";UNTIL 0
90 DO INPUT"WHAT WERE YOU THINKING OF"ST
95 UNTIL LEN T>2
98 L=T; GOSUB s
100 PRINT" TELL ME A Question"
110 PRINT"THAT WILL"'"DISTINGUISH"
120 PRINT "BETWEEN "Sl" AND " Sx '
130 $T="*"; R=T+1
140 INPUT $R; !P=T-TOP; GOSUB s 145 K=T; T=T+8; GOSUB j
150 GOSUB q
_70_
160 K!Q=X-TOP; K!(4-Q)=L-TOP
170 UNTIL 0
1000qINPUT $T
1010 IF ?T=CH"Y"THEN Q=4; RETURN
1020 IF ?T=CH"Q"THEN END
1030 Q=O; RETURN
2000j$T=$R; A=i
2010 DO A=A+1
2020 V=T?(A+4); ST+A+4=""
2030 IF $T+A=" IT "UNTIL 1; GOTO k
2035 T?(A+4)=V
2040 UNTIL A=LEN T-5
2100 PRINT"WHAT WOULD THE ANSWER BE"'
2110 PRINT"FOR " $X
2120 RETURN
2150kT?(A+4)=V; $T+A+1=""
2160 PRINT $T,$X,$T+A+3
2170 RETURN
3000sT=T+LEN T+1; RETURN
9000 REM Set-Up File
9010 T=TOP; ST="*DOES IT HAVE FOUR LEGS"
9015 GOSUB s; P=T; T=T+8; !P=T-TOP
9020 $T="A CROW"; GOSUB s; P!4=T-TOP
9025 $T="A DOG"; GOSUB s
9100zREN Save Tree
9110 F=FOUT "1'
9112 BPUT F,OAA; WAIT
9115 PUT F,(T-TOP-1)
9120 FOR N=TOP TO T-1
9130 RPUT F, ?N
9140 NEXT N
9150 RETURN
Description of Program:
20-30 Load previous tree
23 Look for start flag
35 Reset X to top of tree
50 Print next question
70 Carry on until not a question
75 Guess animal
90-95 Wait for a sensible reply
98 Find end of reply
1000-1030 q: Look for Y, N, or Q; set Q accordingly
2000-2120 j: Look for "IT "in question and print question with "IT"
replaced by name of animal.
3000 s: Move T to end of string $T.
9000 Set up tree file
9100 z: Save tree file.
Variables:
F - Dummy file handle
K - Pointer to addresses of next two branches of tree
L - Pointer to animal typed in
P - Pointer to address of next question or animal.
Q - Value of reply to question; no=0, yes=4.
R - Pointer to question typed in
T - Pointer to next free location
X - Pointer to current position on tree
Program size: 1254 bytes
Additional storage: as required for tree.
_71_
Sample run:
>RUN
ARE YOU THINKING OF AN ANIMAL?Y
DOES IT HAVE FOUR LEGS?Y
CAN YOU RIDE IT?N
DOES IT HAVE STRIPES?N
IS IT A DOG?N
WHAT WERE YOU THINKING OF?A MOUSE
TELL NE A Question THAT WILL
DISTINGUISH BETWEEN A MOUSE AND A DOG
?DOES IT SQUEAK
DOES A DOG SQUEAK?NO
ARE YOU THINKING OF AN ANIMAL?Y
DOES IT HAVE FOUR LEGS?Y
CAN YOU RIDE IT?N
DOES IT HAVE STRIPES?N
DOES IT SQUEAK?Y
IS IT A MOUSE?Y
HO-HO
ARE YOU THINKING OF AN ANIMAL?N
RECORD TAPE
>
_72_
10 More Space and More Speed
This chapter shows how to abbreviate programs so that they will fit
into a smaller amount of memory, and how to write programs so that
they will run as fast as possible.
10.1 Abbreviating BASIC Programs
Most versions of BASIC demand a large amount of redundancy. For
example, the command PRINT must usually be specified in full, even
though there are no other statements beginning with PR. In ATOM BASIC
it is possible to shorten many of the statement and function names,
and omit many unnecessary parts of the syntax, in order to save memory
and increase execution speed. The examples in this manual have avoided
such abbreviations because they make the resulting program harder to
read and understand, but a saving of up to 30% in memory space can be
obtained by abbreviating programs as described in the following
sections.
10.1.1 Statements and Functions
All statement and function names can be abbreviated to the shortest
sequence of characters needed to distinguish the name, followed by a
full stop. The following abbreviations are possible:
Name: Abbreviation:
ABS A.
AND A.
BGET B.
BPUT B.
CH
CLEAR
COUNT C.
DIM
DO
DRAW
END E.
EXT E.
FIN F.
FOR F.
FOUT FO.
GET G.
GOSUB GOS.
GOTO G.
IF
INPUT IN.
LEN L.
LET L.
LINK LI.
LIST L.
LOAD LO.
MOVE
NEW N.
NEXT N.
_73_
OLD
OR
PLOT
PRINT P.
PTR
PUT
REM
RETURN R,
RND R.
RUN
SAVE SA.
SGET S.
SHUT SH.
SPUT SP.
STEP S.
THEN T.
TO
TOP T.
UNTIL U.
WAIT
10.1.2 Spaces
Spaces are largely irrelevant to the operation of the BASIC
interpreter, and they are ignored when encountered in a program. Their
only effect is to cause a 13 microsecond delay in execution. There is
"one place where a space is necessary to avoid an ambiguity as in the
following example:
FOR A=B TO C
where the space after B is compulsory to make it clear that B is not
the first letter of a function name.
10.1.3 LET
Some BASICs demand that every assignment statement begin with the word
LET; e.q.:
LET A=B
In ATOM BASIC the LET statement may be omitted, with a decrease in
execution time.
10.1.4 THEN
The word THEN in the second part of an IF statement may be omitted.
For example:
IF A=B C=D
is perfectly legal. However, note that if the second statement begins
with a T, or a '?' or '!' unary operator, some delimiter is necessary:
IF A=B THEN T=Q
Alternatively a statement delimiter ';' can be used as the delimiter:
IF A=B; T=Q
10.1.5 Brackets
Brackets enclosing a function argument, or an array identifier, are
unnecessary and may be omitted when the argument, or array subscript,
is a single variable or constant.
For example, AA(3) may be written AA3, ABS(RND) may be written
ABSRND, but AA(B+2) cannot be abbreviated.
_74_
10.1.6 Commas
The commas separating elements in a PRINT statement can be omitted
when there is no ambiguity.
For example:
PRINT A,B,C,"RESULT",J
may be shortened to:
PRINTA B C"RESULT"J
Note that the comma in:
PRINT &A,&B
is, however, necessary to distinguish the numbers from the single
number (A&B) printed in hex.
10.1.7 Multi-Statement Lines
Each text line uses one byte per character on the line, plus two bytes
for the line number and a one-byte terminator character; thus writing
several statements on one line saves two bytes per statement. Note
that there are two occasions where this cannot be done:
l. After an IF statement, because the statements on the line following
the IF statement would be skipped if the condition turned out false.
2. Where the line number is referred to in a GOTO or GOSUB statement.
10.1.8 Control Variable in NEXT
The FOR...NEXT control variable may be omitted from the NEXT
statement; the control variable will be assumed to be the one
specified in the most recently activated FOR statement.
10.2 Maximising Execution Speed
ATOM BASIC is one of the fastest BASIC interpreters available, and all
of its facilities have been carefully optimised for speed so that
calculations will be performed as quickly as possible, and so that
real-time graphics programs are feasible.
To obtain the best possible speed from a program the following
hints should be borne in mind; but note that many of these suqgestions
reduce the legibility of the program, and so should only be used where
speed is critical.
l. Use the FOR...NEXT loop in preference to an IF statement and a
GOTO.
2. Use labels, rather than line numbers, in GOTO and GOSUB statements.
3. Avoid the use of constants specified in the body of programs;
instead use variables which have been set to the correct value at the
start of the program. For example, replace:
A=A*1000
by:
T=1000
.
.
A=A*T
4. Write statements in-line, rather than in subroutines, when the
subroutines are only called once, or when the subroutine is shorter
than two or three lines.
_75_
5. If a calculation is performed every time around a loop, make sure
that the constant part of the calculation is performed only once
outside the loop. For example:
FOR J=1 TO 10
FOR K=1 TO 10
VV(K)=VV(J)*2+K
NEXT K
NEXT J
could be written as:
FOR J=1 TO 10
Q=vv(j)*2
FOR K=1 TO 10
VV(K)=Q+K
NEXT K
NEXT J
6. Where several nested FOR...NEXT loops are being executed, and the
order in which they are performed is not important, arrange them so
that the one executed the greatest number of times is at the centre.
For example:
FOR J=1 TO 2
FOR K=1 TO 1000
.
.
NEXT K
NEXT J
is faster than:
FOR K=1 TO 1000
FOR J=1 TO 2
.
.
NEXT J
NEXT K
because in the second case the overhead for setting up the inner loop
is performed 1000 times, whereas in the first example it is only
performed twice.
7. Choose the FOR...NEXT loop parameters so as to minimise
calculations inside the loop. For example:
FOR N=O TO 9
DRAW AA(2*N), AA(2*N+1)
NEXT N
could be rewritten as the faster:
FOR N=O TO 18 STEP 2
DRAW AA(N),AA(N+1)
NEXT N
8. Use word operations rather than byte operations where possible. For
example, to clear the graphics screen to white it is faster to
execute:
_76_
FOR N=#8000 TO #9800 STEP 4; !N=-1; NEXT N
than the following:
FOR N=08000 TO #9800; ?N=-1; NEXT N
9. The IF statement containing several conditions linked by the AND
connective, as, for example:
IF A=2 AND B=2 AND C=2 THEN .....
will evaluate all the conditions even when the earlier ones are false.
Rewriting the statement as:
IF A=2 IF B=2 IF C=2 THEN .....
avoids this, and so gives faster execution.
_77_
_78_
11 Advanced Graphics
The ATOM provides nine different graphics modes, up to a resolution of
256x192 in black and white, and 128x192 in four selectable colours.
The graphics modes use the BASIC statements PLOT, DRAW, and MOVE in an
identical way. All the black-and-white graphics commands are present
in the unexpanded ATOM, although extra memory will be required for the
higher-resolution graphics modes. Colour plotting requires the
addition of an assembler routine, or the COLOUR statement provided in
the extension ROM.
11.1 Graphics Modes
The nine graphics modes are listed below:
Mode: Resolution: Memory:
X: Y:
0 64 48 0.5 K
1a 64 64 1 K
1 128 64 1 K
2a 128 64 2 K
2 128 96 1.5 K
3a 128 96 3 K
3 128 192 3 K
4a 128 192 6 K
4 256 192 6 K
11.2 CLEAR
This statement clears the screen and puts it into graphics
mode. It is followed by a number, or expression in brackets, to
specify the mode. The graphics screen is labelled as follows:
^
|
Y
| |
|
| 0,0 |
-- X --> |
The smallest square which can be plotted on the display is
referred to as a 'pixel' (or 'picture element').
11.3 PLOT
The graphics statements include a versatile 'PLOT K,X,Y' statement,
the value of K determining whether to draw or move, plot lines or
points, whether to set, clear, or invert, and whether to take the
parameters X and Y as the absolute screen position, or as a
displacement from the last point. The values K, X, and Y can be
arbitrarily-complicated expressions.
_79_
K: Function:
0 Move relative to last position
1 Draw line in white relative to last position
2 Invert line relative to last position
3 Draw line in black relative to last position
4 Move to absolute position
5 Draw line in white to absolute position
6 Invert line to absolute position
7 Draw line in black to absolute position
8 Move relative to last position
9 Plot point in white relative to last position
10 Invert point relative to last position
11 Plot point in black relative to last position
12 Move to absolute position
13 Plot point in white at absolute position
14 Invert point at absolute position
15 Plot point in black at absolute position
11.4 DRAW and PDVE
In addition DRAW and MOVE statements are provided as convenient
aliases for drawing a line and moving to an absolute X,Y position.
MOVE X,Y is equivalent to PLOT 12, X, Y.
DRAW X,Y is equivalent to PLOT 5, X, Y.
11.4.1 Random Rectangles
The following program illustrates the use of relative plotting using
the PLOT statement, and draws random rectangles on the display. The
program will work in any of the graphics modes.
10 REM Random Rectangles
13 S=20
16 Z=1;B=O
17 W=64;H=48
18 E=W-S;F=H-S
20 CLEARB
30 FORQ=OT07
32 MOVE(ABSRND%E),(ABSRND%F)
35 C=ABSRND%S+1;D=ABSRNDSS+1;GOSUBs
37 NEXTQ;FOR Q=ot020000;nextq
38 GOT020
100sPLOTZ,C,O
110 PLOTZ, 0, D
120 PLOTZf CfO
130 PLOTZ,O,-D
140 RETURN
Description of Program:
13-18 Set up constants
20 Initialise graphics
30 Draw 41 rectangles
32 Move to random point, leaving margin for size of largest
rectangle.
35 Choose random rectangle
37 Wait; then repeat.
100 140 s: Draw rectangle.
_8O_
Variables:
C,D - Dimensions of rectangle
E,F - Dimensions of safe part of screen to start drawing rectangle.
H - Screen height
Q - Counter
S - Size of squares
W - Screen width
Z - Plot mode; draw relative.
Program size: 278 bytes
11.5 Advanced Graphics Examples
The following examples are designed for use with the higher-resolution
graphics modes, and illustrate some of the applications that are
possible using the ATOM's graphics facilities.
11.5.1 The Sierpinski Curve
This curve is of interest to mathematicians because it has the
property that it encloses every interior point of a square, and yet it
is a closed curve whose area is less than half that of the square.
This program draws successive generations to illustrate how the
Sierpinski curve, which is the limit of these polygonal drawings, is
constructed.
1 REM Sierpinski Curve
10 INPUT"MODE"0
15 INPUT"SIZE"K
20 CLEARO
30 S=5
40 J=l
50 FOR I=1 TO 5
60 J=J*2;D=K/J/4
70 X=K-5*D; Y=K-2*D
80 T=l; MOVE X,Y
90 X=X+D; A=J; B=J; GOTO s
100aIF A=J AND B=J GOTO z
110sP=J; Q=a; R=B
120vIF P<2 goto z
130 if p="2 GOSUB o; GOTO a
140" p="P/2
150 IF Q<p OR P+1<Q GOTO n
170 IF R<P OR P+1<R GOTO n
190 GOSUB c; GOTO a
200nIF Q">=p THEN Q=Q-P
210 IF R>=P THEN R=R-P
220 GOTO v
230zREM end of loop
240 FOR N=1 TQ 1000;NEXT
250 CLEARO
260 NEXT I
270 END 1000cGOTO(1000+100*T)
1100 X=X+D
1105 PLOTS,X,Y
1110 X=X+D;Y=Y+D;PLOTS,X,Y 1120 Y=Y+D;B=B+1;T=4;RETURN
1200 Y=Y-D
1205 PLOTS,X,Y
1210 X=X+D;Y=Y-D;PLOTS,X,Y
_81_
1220 X=X+D;A=A+1;T=1;RETURN
1300 X=X-D
1305 PLOTS,X,Y
1310 X=X-D;Y=Y-D;PLOTS,X,Y 1320 Y=Y-D;B=B-1;T=2;RETURN
1400 Y=Y+D
1405 PLOTS,X,Y
1410 X=X-D;Y=Y+D;PLOTS,X,Y 1420 X=X-D;A=A-1;T=3;RETURN
2000oGOTO(2000+100*T)
2100 X=X+D;PLOTS,X,Y
2110 X=X+D;Y=Y+D;PLOTS,X,Y 2120 X=X+D;Y=Y-D;GOTO 1305
2200' Y=Y-D;PLOTS,X,Y
2210 X=X+D;Y=Y-D;PLOTS,X,Y 2220 X=X-D;Y=Y-D;GOTO 1405
2300 X=X-D;PLOTS,X,Y
2310 X=X-D;Y=Y-9;PLOTS,X,Y 2320 X=X-D;Y=Y+D;GOTO 1105
2400 Y=Y+D;PLOTS,X,Y
2410 X=X-D;Y=Y+D;PLOTS,X,Y 2420 X=X+D;Y=Y+D;GOTO 1205
Description of Program:
50 Plot five generations
l000-1420 Plot centre square
2000-2420 Not a centre square
Variables:
A,B - Coordinates of current square
D - Number of cells in a quarter of a square
J - Number of squares in picture
K - Resolution of screen
0 - Graphics mode
S - Argument for PLOT statement
T - Angle in units of 90 degrees.
X,Y - Current drawing position
Program size: 1047 bytes Sample plot:
_82_
11.5.2 Three-Dimensional Plotting
The following program will plot a perspective view of a
three-dimensional object or curve as viewed from any specified point
in space. The program is simply provided with a subroutine giving the
coordinates of the object to be drawn, or the equation of the curve.
The program below plots a perspective view of the curve
1/(1+x^2+y^2) for a range of values of x and y. The function has been
scaled up by a factor of 300 to bring the interesting part of the
curve into the correct range. The program is provided with an equation
of the curve, specifying z (the vertical axis) in terms of x ,ind y
(the two horizontal axes), and the view position. It Erojccts every
point on the surface onto a plane perpendicular to the line joining
the view position to the origin. The example given here draws line of
equal y, and the surface is drawn as if viewed from the point x=30,
y=40, z=8; i.e. slightly above the surface.
1 REM Three-Dimensional Plotting
50 L=30;M=40;N=8
110 Z=O;CLEAR4
120 A=08000;B=09800
130 FORJ=A TO B STEP4;!J=-1;N.
150 S=L*L+M*M;GOS.s;R=Q
160 S=S+N*N;GOS.s;S=L*L+M*M
170 T=L*L+M*M+N*N
200 F.U=-20TO20
210 V=-20;GOS.c;GOS.b
220 F.V=-19TO20;GOS.c;GOS.a;N.;N.
230 END
400sQ=S/2
410 DOQ=(Q+S/Q)/2
415 U.(Q-1)*(Q-1)<S AND(Q+1)*(Q+1)>S
420 R.
500 REM DRAWTO(UfVfW)
510aZ=3
520k>0=T-U*L-V*M-W*N
530 C=T*(V*L-U*M)*4/(R*0)+128
540 D=96+3*Q*(W*S-N*(U*L+V*M))/(R*0)
560 PLOT(2+4),C,D;Z=O;R.
600cW=300/(10+U*U+V*V)-10;R.
Description of Program:
50 Set up view position
110 Set move mode, and clear screen
120-130 Invert screen
150-170 Calculate constants for linear projection
200-230 Scan X,Y plane evaluating function and plotting projected lines.
400-420 s: Square root routine (see Section 5.2.2).
500-560 a: Calculate projected position of next point and move to it
(Z=O) or draw to it (Z=3)
600 c: Function for evaluation
Variables:
A - Display area start
B - Display area end
C,D - Coordinates of projected point
J - Display location to be cleared
Q,r,s,t - Constants for projection
U,V - Scan variables
_83_
W - Function value
Program size: 491 bytes
Sample Plot
11.6 Plotting Hex Characters
In the higher graphics modes, modes 1 to 4, characters cannot be
plotted on the screen directly but it is fairly simple to draw
characters using the graphics statements. The following simple
routines will draw the hex characters 0 to F, with any desired
scaling, and with an optional slope. The routines are useful for
labelling graphs drawn in the higher-resolution qraphics modes.
Routine p plots a single hex character; routine q plots two hex
characters. The routine is demonstrated by drawing random hex
characters in a circle.
1 REM Plotting Hex Characters
10 N=TOP; !N=06E3E4477; N!4=0467B6B4D
12 N!8=f795F4F7F; N!12=01B3B7C33
20 V=2; H=2; S=O
25 CLEAR 0
30 X=30; Y=O
40 MOVE (32+X),(24+Y)
50 X=X+Y/6;Y=Y-X/6
60 A=ABSRND&OF
70 GOSUBp
90 GOTO 40
1000qREN Plot B as 2 hex digits
1010 A=B/16; GOSUB p
1020 A=B&#F
2000pREM Plot A in hex
2001 REM uses:A,H,J,K,L,N,Q,V
2010 Q=n?a
2020 FOR J=1 TO 7
2030 K=(2-J%6)%2;L=(2-(J'-1)%4)%2
2040 PLOT(Q&1),(L*H+K*S),(K*V)
2050 Q=Q/2; NEXT J
2060 PLOTO,((H+2)/2),0; RETURN
_84_
Description of Program:
10-12 Set up plotting statements for the 16 characters.
20 Scales for letters
30-50 Move X,Y around a circle
60-70 Plot random character
1000-1020 q: Plot low-order byte of B as two hex digits
2000-2060 p: Plot low-order hex digit of A in hex
Variables:
A - Hex digit to be plotted
B - Byte to be plotted
H - Horizontal scaling
N - Vector containing character plotting statements
Q - Next plot statement; low-order bit determines whether to draw or
move.
S - Slope factor
V - Vertical scaling
X,Y - Coordinates of point on circle.
Program size: 457 bytes Vector: 16 bytes
11.7 Animated Graphics
The graphics statements are optimised for speed. For example, to draw
a diagonal across the screen using:
MOVE O,O ; DRAW 255,191
takes under 40 msec. The following program uses animated graphics to
display a clock whose hands move to show the correct time. The hands
are drawn using the statement PLOT 6, and the same statement is
repeated to remove each hand’s old position before drawing its new
position. The clock keeps accurate time by executing the WAIT
statement:
1 REM Clock
10 CLEAR4;E=128;F=96
15 J=71;K=678;Q=100;R=OB001
20 X=O;Y=8000;G=90
30 MOVE(X/Q+E),(Y/Q+F)
40 FORL=O TO 59
45 IF L%5<>0 GOTO c
50 DRAW(X/G+E),(Y/G+F)
55 MOVE(X/Q+E),(Y/Q+F)
60cGOSUBi;GOSUBp
68 NEXTL
70 X=O;Y=5000;S=O
72 DO A=O;B=6600
80 FOR H=O TO 4
82 GOSUBh;C=X;D=Y;X=A;Y=B
84 FOR M=O TO 11
85 GOSUBh;A=X;B=Y
87 X=O;Y=7000
88 IF ?R<>OFF GOTO b
90 FOR L=O TO 59
110 GOSUB s
120 FOR N=S TO 55;WAIT;NEXT N 130 S=O
140 GOSUBs;GOSUBi
150 NEXT L
155bX=A;Y=B
160 GOSUBh;GOSUBi
_85_
170 NEXT M
175 A=X;B=Y;X=C;Y=D
180 GOSUBh;GOSUBi
200 NEXT H; UNTIL 0
399 REM
400h510VE E,F
410 V=X/2/Q;U=Y,¿2’Q;W=Vj5;T=U/5
415 WAIT
420 PLQT6,(V-T+E),(U+W+F)
430 PLOT6,(X/Q+E),(Y/Q+F)
440 PLOT6,(V4T+E),(U-W+F)
450 PLOT6,E,F;S=S+5;RETURN
500iWAIT;X=X+J*Y/K
510 Y=Y-J*X/K;S=S+1;RETURN
600sMOVE E,F
620pWAIT;PLOT6,(X/Q+E),(Y/Q+F)
630 S=S+1;RETURN
Description of Program:
40-68 Draw clock face
80-84 Do hours and minutes
88 If shift key down miss out seconds
90-150 Do seconds
120 Use up remainder of each second
400-450 h: Draw hour/minute hand from centre of screen to X,Y
500-510 i: Increment X,Y one sixtieth of way around circle.
600 s: Draw second hand
620-630 p: Plot to point X,Y
Variables:
A,B - Coordinates of tip of minute hand
C,D - Coordinates of tip of hour hand
E,F - Coordinates of centre of screen
H - Twelves of minutes counter
J,K - Incremental variables; J/K = 2*PI/60 approx.
L - Seconds counter
M - Minutes counter
N - Counter
Q - Scaling factor
R - Address of shift key
S - Sixtieths of a second used out of current second
X,Y - Coordinates on screen scaled by Q
Program size: 806 bytes
_86_
Sample Plot:
To set the correct time hold the shift key down after typing RUN, and
release it when the hour and minute hands are in the correct
positions.
11.8 Plotting in BASIC
To illustrate how the plotting statements work, the following BASIC
programs will plot points on the screen in the different graphics
modes without using PLOT, DRAW, or MOVE.
11.8.1 Plotting and Testing Points in Mode 0
The following BASIC program will plot a point in the graphics mode 0;
the main program sets up a vector V which contains bytes with a single
bit set to denote the bit to be plotted. Subroutine p plots a point at
the coordinates X and Y.
1 REM Plot in Mode 0 10 DIM V(5)
20 !V=#04081020; V!4=#102
100 REM Plot point at X,Y
110 REM Changes: P; Uses V,X,Y
120pP=X/2+(47-Y)/3*32+#8000
130 ?P=?P\IV?(X&1+(47-Y)%3*2);RETURN
Using this method it is possible to determine the state of any point
on the screen, as well as actually plotting points. For example,
changing line 130 to:
130 Q=(?p&(v?(x&1+(47-y)%3*2))<>0)
uses Q as a logical variable whose value is set to ’true' if the point
X,Y is set, and to 'false' if the point is clear.
Note that the screen should be cleared by writing 040 in every
location (or with the statement CLEAR 0) before plotting in graphics
mode zero with this routine.
_87_
11.8.2 Plotting in Higher Graphics Modes
To set the ATOM to a higher graphics mode the following character
should be stored in location #BOOO:
Mode: Value:
0 #00
1a #10
1 #30
2a #50
2 #70
3a #90
3 #B0
4a #DO
4 #F0
This operation is performed automatically for modes 0, 1, 2, 3, and 4
by the CLEAR statement. Modes la, 2a, 3a, and 4a are colour graphics
modes; see section 11.9 below.
To illustrate plottivg in the higher modes the following BASIC
program will plot a point on the screen at the coordinates X,Y in the
highest-resolution graphics mode:
10 DIM V(7)
20 !V=410204080; V!4=#1020408
30 ?#B000=#F0
100 REM Plot point at X,Y
110 REM Changes: P; Uses: V,X,Y
1OOpP=X/8+(191-Y)*32+#8000
102 ?P=?\V?(X&7);RETURN
Again the program can be modified to test the state of points of the
screen.
11.9 Colour Graphics
The ATOM provides three additional graphics modes which provide
graphics in four selectable colours up to a maximum definition of
128x192. These modes are known as la, 2a, 3a, and 4a. The BASIC's
PLOT, DRAW, and MOVE statements can be used in the 4-colour modes
provided that a point-plotting routine, written in assembler, is
provided to replace the black-and-white point plotting routines.
Alternatively the COLOUR statement, provided in the extension ROM, can
be used; see Section 22.2. The address of the point-plotting routine
used by PLOT, MOVE, and DRAW is stored in RAM at 03FE and 03FF. The
following information is passed down to the point-plotting routine in
zero page:
Location: Function:
5A X coordinate - low byte
5B " " high byte
5C Y coordinate - low byte
5D " " high byte
5E 1: set bit, 2: invert bit, else, clear bit.
5F Free for workspace
60 " "
The following BASIC program demonstrates how an assembler
point-plotting routine can be provided to give four-colour plotting in
graphics mode 4a, the highest-resolution colour graphics mode:
_88_
10 REM 4-Colour Plot
12 GOSUB 400
16 CLEAR4;?4BOOO=ODO
18 ?03FE=Q;?03FF=Q&OFFFF/256
30 FOR J=O TO 64 STEP 2
40 ?C=J%3*4;MOVE J,O
50 DRAW 127,J;DRAW(127-J),191
60 DRAW 0,(191-J);DRAW J,O
70 NEXT J
80 END
400 DIM V(11),C(0),P(-1),Q(-1)
420 !V=#01041040;V!4=002082080;V!8=#030C30CO 430 P.$21
508[
510 LDA@O;STA #5F
520 LDA#5C;LSR A;ROR #5F
530 LSRA;ROR#5F;LSRA;ROR#5F
540 STA#60;LDA#5A;LSRA;LSRA
550 CLC;ADC#5F;STA05F
560 LDA#60;ADC@#80;STA#60
570\#5f AND #60 CONTAIN ADDRESS
580 LDA05A;AND@3;CLC;ADCC;TAY
590 LDX@0;LDAV,Y;ORA(#5F,X)
600 STA(#5F,X);RTS
610]
620 P.$6
630 RETURN
Description of Program:
12 Assemble point plotting routine
16 Clear display; set mode 3a
18 Change point plotter vector
30-70 Demonstration program; curve stitching in 4 colours
400 Set up variable space
420 Vectors for three colours
430 Disable assembler listing
508-610 Assembler point-plotter program 620 Turn screen back on
Variables:
C - Colour: 0, 4, or 8.
P - Location counter
Q - Address of point-plotting routine
V - Vectors for setting bits
Program size: 558 bytes Vectors: 13 bytes
Note that the routine only sets bits, and plots in three colours - the
fourth colour being the background colour. It would be a simple matter
to modify the routine so that it was able to set or unset bits; i.e.
plot in the background colour.
_89_
_90_
12 What to do if Baffled
This section is the section to read if all else fails; you have
studied your program, and the rest of the manual, and you still cannot
see anything wrong, but the program refuses to work.
There are two types of programming errors; errors of syntax, and
errors of logic.
12.1 Syntax Errors
Syntax errors are caused by writing something in the program that is
not legal, and that is therefore not understood by the BASIC
interpreter. Usually this will give rise to an error, and reading the
description of that error code in Chapter 27 should make the mistake
obvious.
Typical causes of syntax errors are:
1. Mistyping a digit '0' for a letter '0', ard vice-versa. E.g.:
FOR N=1 TO 3
2. Mistyping a digit '1' for a letter 'I’, and vice-versa. E.g.:
1F J=2 PR1NT "TWO"
3. Forgetting to enclose an expression in brackets when it is used as
a parameter in a statement. E.g.:
MOVE X+32,Y
In some cases a syntax error is interpreted as legal by BASIC, but
with a different meaning from that intended by the programmer, and no
error message will be given. E.g.:
MOVE 0,0
was intended to move to the origin, but in fact moves to some
coordinates dependent on the value of the variable 0.
12.2 Logical Errors
Errors of logic arise when a program is perfectly legal, but does not
do what the programmer intended, probably because the programmer
misinterpreted something in this manual, or because a situation arose
that was not forseen by the programmer. Common logical errors are:
l. Unitialised variables. Remember that the variables A-Z initially
contain unpredictable values, and so all the variables used in a
program should appear on the left hand side of an assignment
statement, in an INPUT statement, dimensioned by a DIM statement, or
as the control variable in a FOR...NEXT loop, at least once in the
program. These are the only places where the values of variables are
changed.
2. The same variable is used for two purposes. It is very easy to
forget that a variable has been used for one purpose at one point in
the program, and to use it for another purpose when it was intended to
save the variable's original value. It is good practice to keep a list
of the variables used in a program, similar to the list given after
_91_
the application programs in this manual, to avoid this error.
3. Location counter P not set up when assembling. The value of P
should be set before assembling a program to the address of an unused
area of memory large enough to receive the machine code, and P should
not be used for any other purpose in the program.
4. Graphics statements used without initialising graphics. The CLEAR
statement must precede use of any graphics statements.
5. Assigning to a string variable and exceeding the allocated space.
Care should be taken that enough space has been allocated to string
variables, with DIM, to receive the strings allocated to them.
6. Assigning outside the bounds of an array or vector. Assigning to
array or vector elements above the range dimensioned in the DIM
statement will overwrite other arrays, vectors, or strings.
12.3 Suspected Hardware Faults
This section deals with faults on an ATOM which is substantially
working, but which exhibits faults which are thought to be due to
hardware faults rather than programming faults. Hardware fault-finding
details are provided in the Technical Manual; this section describes
only those hardware problems that can be tested by running software
diagnostics.
12.3.1 RAM Memory Faults
The fallowing BASIC program can be used to verify that the ATOM's
memory is working correctly:
1 REM MEMORY TEST
10 INPUT"FROM"A," TO"B
20 DO ?12=0; R=!8
30 FOR N=A TO B STEP4;!N=RND; NEXT N
35 ?12=0; !8=R
40 FOR N=A TO B STEP4
50 IF !N<>RND PRINT'"FAIL AT "&N'
60 NEXT N
70 P." OK"; UNTIL 0
The first address entered should be the lowest address to be tested,
and the second address entered should be four less than the highest
address to be tested. For example, to test the screen memory enter:
>RUN
FROM?#8000
TO?#81FC
The program stores random numbers in the memory locations, and then
re-seeds the random-number generator and checks each location is
correct.
12.3.2 ROM Memory Faults
The BASIC interpreter, operating system, and assembler, are all
contained in a single 8K ROM, and as all ROMs are thoroughly tested
before despatch it is very unlikely that a fault could be present.
However, if a user suspects a ROM fault the following program should
be entered and run; the program obtains a 'signature' for the whole
ROM, this signature consistinq of a four-digit hexadecimal number. The
program should be run for each 4K half of the ROM.
_92_
1 REM CHC Signature
10 INPUI' "LOOM ADDRESS", P
20 C=O;Z=OFFFI';Y=#2D
30 FOR 0=0 TO #FFF
35 A=P?Q
40 FOR B=l TO 8
60 C=C*2+A&1;A=A/2;IFC>Z C=C:Y;C=C&Z
80 NEXT B; NFXT Q
110 PRINT "SIGNATURE IS" &C'
120 END
Program size: 213 bytes Sample run:
>RUN
PROM ADDRESS?#COOO
SIGNATURE IS D67D
>RUN
PROM ADDRESS?#FOOO
SIGNATURE IS E386
The program takes about 6 minutes to run, and if these signatures are
obtained the ROM is correct.
The Atom extension ROM, described in chapter 22, can be tested by
giving the reply #DOOO to the prompt. It should give a signature of
AAA1.
12.3 Programming Service
If all else fails, owners of an ATOM may make us¿ of the free
Programming Service provided by Acorn. To ensure a rapid reply to any
queries the special Programming Service Forms, supplied with the ATOM,
must be used to submit the problem New forms will be supplied with
the reply to any queries, or on request.
All reports should be accompanied by a full description of the
problem or fault, and the occasions when it occurs. Please also
enclose a stamped addressed envelope for the reply. A program should
be supplied which illustrates the problem or suspected fault. This
program should preferably be only four or five lin s long, and should
be written in the space provided on the Programming Service Form, with
any spaces in the original carefully included. If the problem or fault
is only exhibited by a longer program the report form should be
accompanied by a cassette tape recording of the program, and the title
of the file on the tape should be entered on the form. The cassette
will be returned with the reply.
_93_